Question

Consider a binary classification problem where each example (observation) x has n features and class label y can take one of the two possible values: y = 1 (positive class label) and y = 0 (negative class label). Suppose a Logistic Regression model is trained using a training set and θ ∈ Rn is the learned parameter vector of this trained model. Show that given an unseen example x ∈ Rn having n features, the trained Logistic Regression model will predict its class label to be 1, if θ⊤x > 0 and class label to be 0 otherwise.

Answer 1

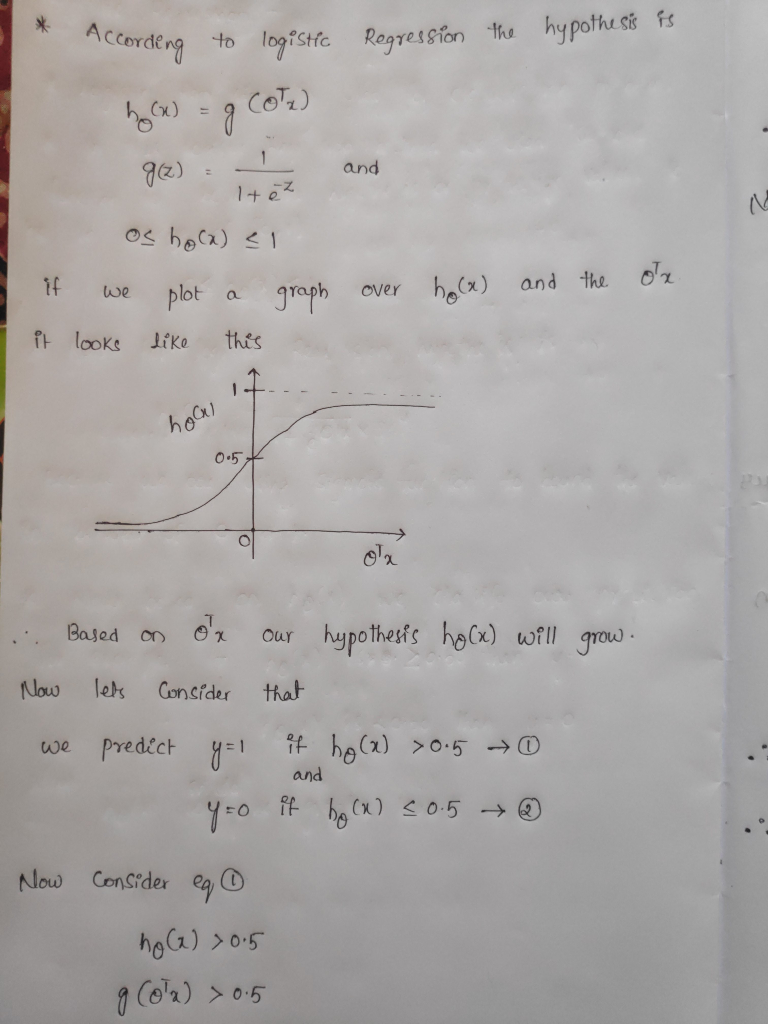
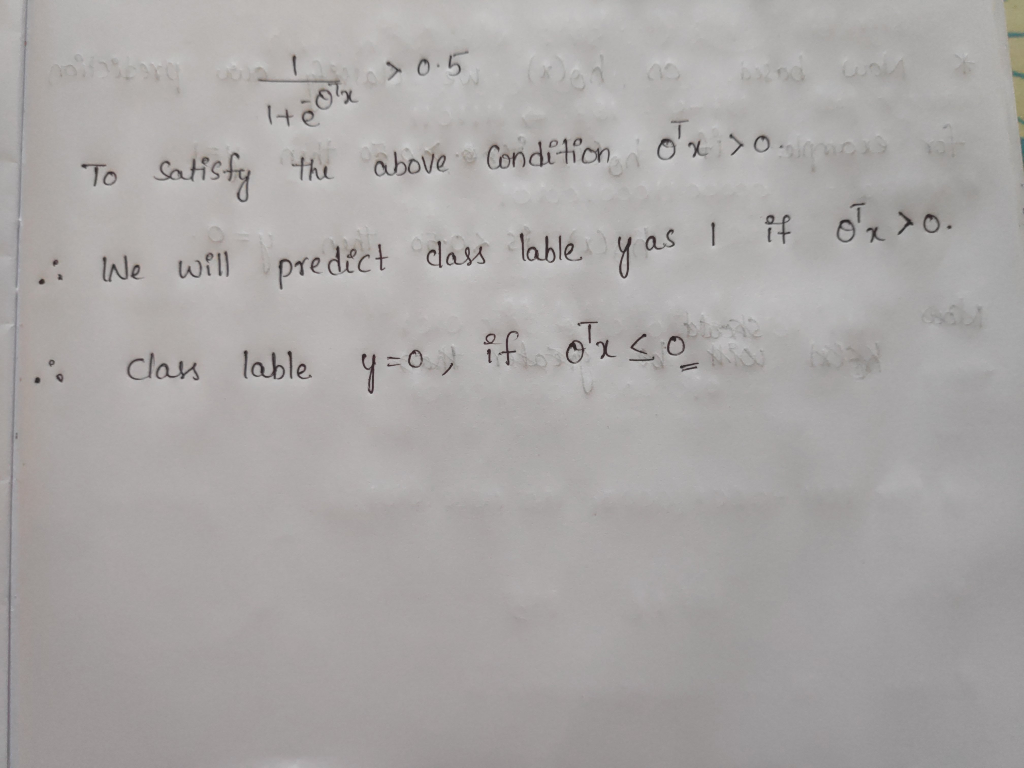Here the function is predicting the values of class lable.This values should be in [0,1].

Now we consider y-lable as 1 if the >0.5 and

y-lable as 0 if <= 0.5

Let's consider that our prediction > 0.5 then y-lable is 1.

But >0.5 if and only if is >0 and   is >= 1 if >0