Consider the random experiment of tossing two fair dice and recording the up faces. Let X...

Consider the random experiment of tossing two fair dice and recording the up faces. Let X be the sum of the two dice, and let Y be the absolute value of the difference of the two dice.

1.Compute the skewness coefficient and kurtosis of the distribution of X and Y.

2. For each of x=4,5,6 from the sample space of X do the following:

Construct the pff of the conditional distribution of X given Y = y

Compute the mean variance SD skewness coefficient snd kurtosis of the conditional distribution of Y given X = x. Are they distributional characteristics constant, or do they depend upon x?

Expert Solution

Dear student this is a huge time consuming question.. But I did it only to help you... Your satisfaction is more important to me.. If you are satisfied Please THUMBS UP and Support me... Thanks..

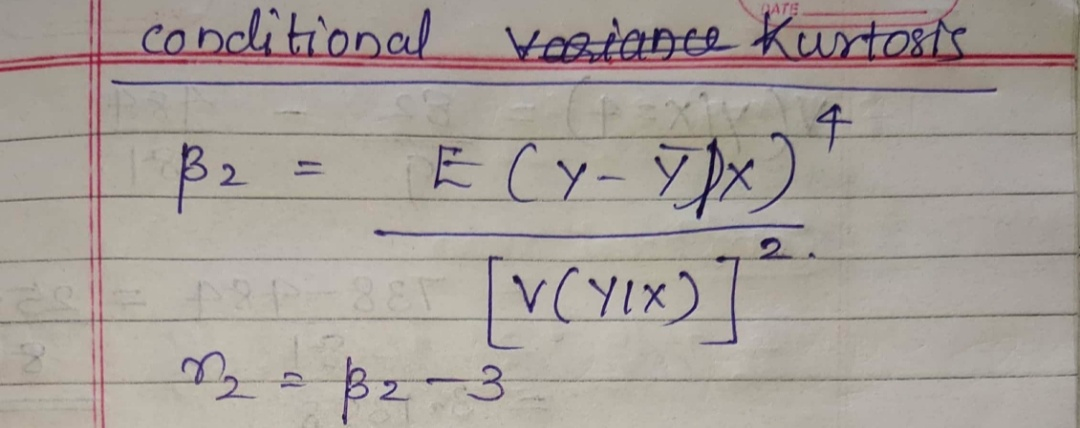
You can clearly see all distributional characteristics are constant..

milcah answered 1 hour ago

Let a random experiment consist of tossing two fair six sided dice. Let x be the...

Let a random experiment consist of tossing two fair six sided dice. Let x be the minimum number shown on the dice. Determine the closed form PMF of x. Hint: Creating a chart for all possible combinations of the two rolls may be helpful.

Consider the experiment of tossing two dice. Your random variable is D, the square of difference...

Consider the experiment of tossing two dice. Your random variable is D, the square of difference of the numbers showing on the faces of the two dice. Show its probability distribution in the form of a table. Find the mean, median and mode of the distribution. Find the variance of D. What type of skewness does the probability distribution represent? Is the Chebychev inequality satisfied for c=1 and c=2? Show the calculations.

Consider the experiment of tossing two dice. Your random variable is D, the square of difference...

Consider the experiment of tossing two dice. Your random variable is D, the square of difference of the numbers showing on the faces of the two dice. Show its probability distribution in the form of a table. Find the mean, median and mode of the distribution. Find the variance of D. What type of skewness does the probability distribution represent? Is the Chebychev inequality satisfied for c=1 and c=2? Show the calculations.

Consider the experiment of tossing two dice. Your random variable is D, the square of difference...

Consider the experiment of tossing two dice. Your random variable is D, the square of difference of the numbers showing on the faces of the two dice. Show its probability distribution in the form of a table. Find the mean, median and mode of the distribution. Find the variance of D. What type of skewness does the probability distribution represent? Is the Chebychev inequality satisfied for c=1 and c=2? Show the calculations.

Let X be the random variable for the sum obtained by rolling two fair dice. (1)...

Let X be the random variable for the sum obtained by rolling two fair dice. (1) What is the probability density function? (2) What is the cumulative probability density function? (3) What is the expected value? (4) What is the variance?

Roll two fair dice. Each die has six faces. A. Let A be the event that...

Roll two fair dice. Each die has six faces. A. Let A be the event that either a 3 or 4 is rolled first followed by an odd number. P(A) = Round your answer to two decimal places. B. Let B be the event that the sum of the two dice is at most 7. P(B) = Round your answer to two decimal places. C. Are A and B mutually exclusive events? (Yes or No) D. Are A and B independent or...

Question

Consider the random experiment of tossing two fair dice and recording the up faces. Let X...

Solutions

Expert Solution

Related Solutions

Let a random experiment consist of tossing two fair six sided dice. Let x be the...

Consider the experiment of tossing two dice. Your random variable is D, the square of difference...

Consider the experiment of tossing two dice. Your random variable is D, the square of difference...

Consider the experiment of tossing two dice. Your random variable is D, the square of difference...

Let X be the random variable for the sum obtained by rolling two fair dice. (1)...

Roll two fair dice. Each die has six faces. A. Let A be the event that...

suppose two dice are tossed. let x= the sum of the on the top faces of...

Consider rolling two dice and let (X, Y) be the random variable pair defined such that...

Two fair dice are rolled. Let X be the product of the number of dots that...

2. Roll a pair of unbiased dice. Let X be the maximum of the two faces...