Question

8) How do you know if a given force is conservative? Carefully explain how you would go about defining a potential function for a given conservative force (be sure to explain briefly the significance of the choice of reference point).

Answer 1

There are four well-known, equivalent tests to determine if a force is conservative:  the curl is zero, a potential function whose gradient is the force exists, all closed path integrals are zero, and the path integral between any two points is the same no matter what the path chosen.  In this notebook, quaternion operators perform these tests on quaternion-valued forces

There Exists a Potential Function for the Force

Operate on force quaternion using integration.  Take the negative of the gradient of the first component.  If the field quaternion is the same, the force is conservative.

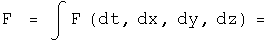
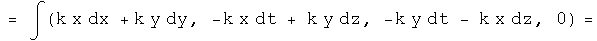
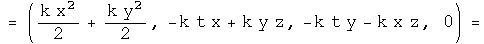
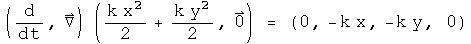
This is the same force as we started with, so the scalar inside the integral is the scalar potential of this vector field.  The vector terms inside the integral arise as constants of integration.  They are zero if t=z=0.  What role these vector terms in the potential quaternion may play,