Question

Allegiant Airlines charges a mean base fare of $89. In addition, the airline charges for making a reservation on its website, checking bags, and inflight beverages. These additional charges average $35 per passenger. Suppose a random sample of 80 passengers is taken to determine the total cost of their flight on Allegiant Airlines. The population standard deviation of total flight cost is known to be $38. Use z-table.

b. What is the probability the sample mean will be within $10 of the population mean cost per flight (to 4 decimals)?

c. What is the probability the sample mean will be within $5 of the population mean cost per flight (to 4 decimals)?

Answer 1

X : Cost per flight

Given

Population standard deviation of total flight cost is known to be $38

Number of passengers in the random sample : n = 80

Sampling distribution of sample mean : follows normal distribution with mean same as that of X and standard deviation

b.

Probability the sample mean will be within $10 of the population mean cost per flight

Z-score for = mean -10 = (mean -10 -mean)/4.2485 = -10/4.2485 = -2.35

Z-score for = mean +10 = (mean +10 -mean)/4.2485 = 10/4.2485 = 2.35

From standard normal tables,

P(Z-2.35) = 0.0094

P(Z2.35) = 0.9906

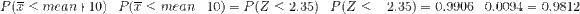
Probability the sample mean will be within $10 of the population mean cost per flight = 0.9812

c.

Probability the sample mean will be within $5 of the population mean cost per flight

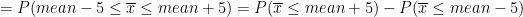
Z-score for = mean -5 = (mean -5 -mean)/4.2485 = -5/4.2485 = -1.18

Z-score for = mean +5 = (mean +5 -mean)/4.2485 = 5/4.2485 = 1.18

From standard normal tables,

P(Z-1.18) = 0.1190

P(Z1.18) = 0.8810

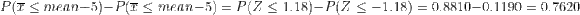
Probability the sample mean will be within $5 of the population mean cost per flight = 0.7620