Question

An ethylene glycol solution contains 21.2 g of ethylene glycol (C₂H₆O₂) in 89.4 mL of water. (Assume a density of 1.00 g/mL for water.)

Determine the boiling and freezing point of the solution. Express you answer in degrees Celsius.

Answer 1

Number of moles of ethylene glycol (C₂H₆O₂)=2xMolar mass of C+6xMolar mass of H+2xMolar mass of O

=2x12 g/mol+6x1 g/mol+2x16 g/mol

=24 g/mol+6 g/mol+32 g/mol

=62 g/mol

Number of moles of ethylene glycol=mass of ethylene glycol/molar mass of ethylene glycol

=21.2 g/62 g/mol=0.34 mol

Mass of water=Volume x density

=89.4 mL x 1.00 g/mL=89.4 g

Molality of given solution=number of moles of ethylene glycol/mass of water (kg)

=0.34 mol/(89.4 g/1000 g/kg) (1 kg=1000 g)

=3.8 m

Freezing point of pure water=0°C

Freezing point depression constant for water=K_f=1.86 °C/m

We know that freezing point depression is given as

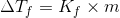
Where m=Molality of solution

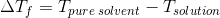=K_f x m

Here T_{pure solvent}=freezing point of pure water=0°C

T_solution =Freezing point of solution

0°C-T_f=1.86°C/m x 3.80 m=7.1°C

T_f=0°C-7.1°C=-7.1°C

So freezing point of given solution=-7.1°C

Boiling point of pure water=100°C

Boiling point elevation constant for water=K_b=0.512 °C/m

Elevation in boiling point is given as

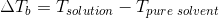=K_b x m

Where T_solution=Boiling point of solution

T_{pure solvent}=Boiling point of pure water =100°C

m=Molality of solution

T_b-100°C=0.512°C/m x 3.8 m=1.9 °C

T_b=1.9°C+100°C=101.9°C

So boiling point of given solution=101.9°C