Question

A borrower takes out a 30-year price level adjusted mortgage loan for $200,000 with monthly payments. The initial interest rate is 4% with 4 points. Assuming that inflation is expected to increase at the rate of 3% for the next 5 years, and a fully amortizing loan is made.

What is the inflation adjusted loan balance at the end of year 2? (Choose the nearest number)

	a.	$ 202,372
	b.	$ 198,597
	c.	$ 196,478
	d.	$ 204,555

What is the expected effective yield to the lender if the loan is repaid in 2 years? (Choose the nearest number)

	a.	9%
	b.	6%
	c.	7%
	d.	12%

Answer 1

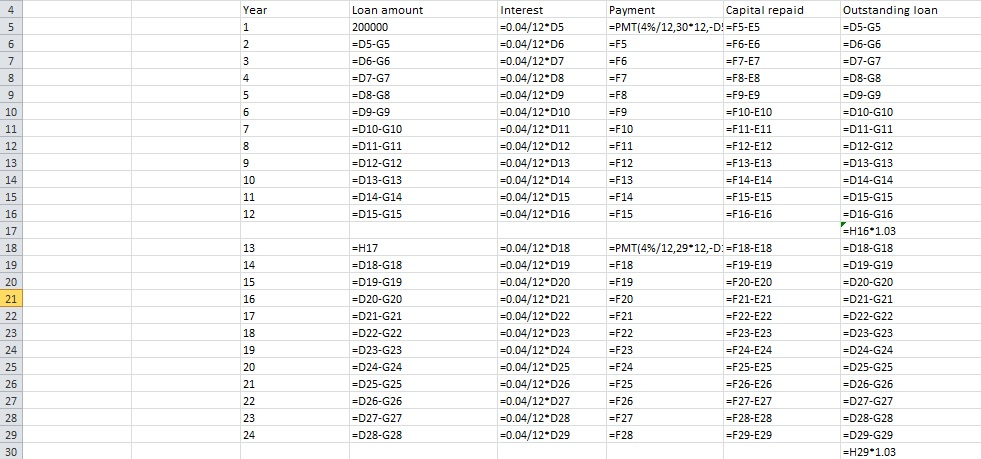
Option d is correct.

Year	Loan amount	Interest	Payment	Capital repaid	Outstanding loan
1	200000	666.6667	$954.83	$288.16	$199,711.84
2	$199,711.84	665.7061	$954.83	$289.12	$199,422.71
3	$199,422.71	664.7424	$954.83	$290.09	$199,132.62
4	$199,132.62	663.7754	$954.83	$291.06	$198,841.57
5	$198,841.57	662.8052	$954.83	$292.03	$198,549.54
6	$198,549.54	661.8318	$954.83	$293.00	$198,256.54
7	$198,256.54	660.8551	$954.83	$293.98	$197,962.57
8	$197,962.57	659.8752	$954.83	$294.96	$197,667.61
9	$197,667.61	658.892	$954.83	$295.94	$197,371.67
10	$197,371.67	657.9056	$954.83	$296.93	$197,074.75
11	$197,074.75	656.9158	$954.83	$297.91	$196,776.83
12	$196,776.83	655.9228	$954.83	$298.91	$196,477.93
					$202,372.26
13	$202,372.26	674.5742	$983.48	$308.90	$202,063.36
14	$202,063.36	673.5445	$983.48	$309.93	$201,753.43
15	$201,753.43	672.5114	$983.48	$310.96	$201,442.47
16	$201,442.47	671.4749	$983.48	$312.00	$201,130.47
17	$201,130.47	670.4349	$983.48	$313.04	$200,817.43
18	$200,817.43	669.3914	$983.48	$314.08	$200,503.34
19	$200,503.34	668.3445	$983.48	$315.13	$200,188.21
20	$200,188.21	667.294	$983.48	$316.18	$199,872.03
21	$199,872.03	666.2401	$983.48	$317.24	$199,554.80
22	$199,554.80	665.1827	$983.48	$318.29	$199,236.50
23	$199,236.50	664.1217	$983.48	$319.35	$198,917.15
24	$198,917.15	663.0572	$983.48	$320.42	$198,596.73
					$204,554.63

2. Using excel, IRR function is

Year	CF
0	-200,000
1	$954.83
2	$954.83
3	$954.83
4	$954.83
5	$954.83
6	$954.83
7	$954.83
8	$954.83
9	$954.83
10	$954.83
11	$954.83
12	$954.83
13	$983.48
14	$983.48
15	$983.48
16	$983.48
17	$983.48
18	$983.48
19	$983.48
20	$983.48
21	$983.48
22	$983.48
23	$983.48
24	$205,538.11
IRR =	0.57%

Effective annual yield = (1 + 0.57%)^12- 1

Effective annual yield = 0.07 or 7%

Option c is correct.