Question
In: Computer Science
Problem 14.1.2 Let M be a DFA with transition function δ. Prove carefully, by induction for...
Problem 14.1.2 Let M be a DFA with transition function δ. Prove carefully, by induction for all strings w over M’s alphabet, that δ ∗ (i, w) = j if and only if there is a path from node i to node j in the graph of M such that the labels on the edges of the path, read in order, form w.
Solutions
Expert Solution
Base case :- |w| = 1.
Let w= a.
Then 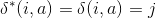
Clearly for |w|= 1, 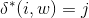 only if there is path (which is single edge in this case) in graph
of M from i to j with label of edge being single letter w
itself.
only if there is path (which is single edge in this case) in graph
of M from i to j with label of edge being single letter w
itself.
Hence the statement is true for base case.
Induction hypothesis :- 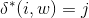 if and only if there is path from i to j in the graph of M with
labels on the edges of path in order form string w and |w| <=
k.
if and only if there is path from i to j in the graph of M with
labels on the edges of path in order form string w and |w| <=
k.
Inductive step :- |w| = k+1
Let w = w'c where 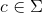
Now if 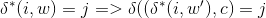
Since |w'| = k. If 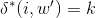 then as per induction hypothesis , there must be path from node i
to node k in graph of M with labels of edges being alphabets in w'
from left to right.
then as per induction hypothesis , there must be path from node i
to node k in graph of M with labels of edges being alphabets in w'
from left to right.
Now, 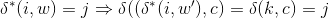
This means that there is path from node i to node k and then there is an edge from node k to node j with label of edge being alphabet c. This means that there is path from node i to node j of length k+1.
Hence the argument that 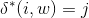 if and only if there is path from node i to node j in the graph of
M satisfied even for |w|=k+1 which proves that given statement is
correct for all string w.
if and only if there is path from node i to node j in the graph of
M satisfied even for |w|=k+1 which proves that given statement is
correct for all string w.
Please comment for any clarification .
Related Solutions
Prove that the language L={(M, N): M is a Turing machine and N is a DFA...
In this problem we prove that the Strong Induction Principle and Induction Principle are essentially equiv-...
Use induction to prove Let f(x) be a polynomial of degree n in Pn(R). Prove that...
Prove by Induction. Prop: if the (greatest common factor) gcf(a,m) = f then there is k,...
Linear Algebra Carefully prove the following statement: Let A be an n×n matrix. Assume that there...
Use double induction to prove that (m+ 1)^n> mn for all positive integers m; n
C. Prove the following claim, using proof by induction. Show your work. Let d be the...
Let f : R → R be a function. (a) Prove that f is continuous on...
Let N be a submodule of the R-module M. Prove that there is a bijection between...
Let f be a one-to-one function from A into b with B countable. Prove that A...
- Biology/ anatomy of the human body Briefly discuss three structural and two functional characteristics common to...
- Suppose that a certain random variable, X, has the following cumulative distribution function (cdf): F(x) =...
- Who are the mercantilists? 2. What policies did they advocate and how did they expect these...
- Please Answer with C code and I will rate! Thank you. Problem) Write a program that...
- You want to determine the concentration of Fe2+in a solution. You decide to determine the Fe2+...
- Part A. Plank‘s constant Plank‘s constant has units of Joules times second (Js). (a)Perform a dimensional...
- 1. what is the difference between sole proprietorships and partnerships?briefly 2. what is the components balance...
 venereology answered 2 months ago
venereology answered 2 months ago