Question
In: Math
A report from the U.S. Department of Agriculture shows that the mean American consumption of carbonated...
A report from the U.S. Department of Agriculture shows that the mean American consumption of carbonated beverages per year is greater than 52 gallons. A random sample of 30 Americans yielded a sample mean of 69 gallons. Assume that the population standard deviation is 20 gallons, and the consumption of carbonated beverages per year follows a normal distribution. Calculate a 95% confidence interval, and write it in a complete sentence related to the scenario.
Solutions
Expert Solution
Solution :
Given that,
sample mean =  = 69
= 69
Population standard deviation =  = 20
= 20
Sample size = n =30.
At 95% confidence level the z is ,
 = 1 - 95% = 1 - 0.95 = 0.05
= 1 - 95% = 1 - 0.95 = 0.05
 / 2 = 0.05 / 2 = 0.025
/ 2 = 0.05 / 2 = 0.025
Z /2
= Z0.025 = 1.96
/2
= Z0.025 = 1.96
Margin of error = E = Z /2
* (
/2
* ( 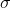 /
/n)
= 1.96* ( 20 / 30
)
= 7.16
At 95% confidence interval
is,
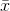 - E <
- E <  <
< 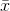 + E
+ E
69 - 7.16 <  < 69 + 7.16
< 69 + 7.16
61.84<  <76.16
<76.16
lower limit 61.84
upper limit 76.16
sample mean fall between lower and upper limits
( , )
Related Solutions
The U.S. Department of Agriculture claims that the mean consumption of bottled water by a person...
According to Food Consumption, Prices, and Expenditures, published by the U.S. Department of Agriculture, the mean...
3. The U.S. Department of Agriculture claims that the mean cost of raising a child from...
The average American consumed 10.6 pounds of mozzarella cheese in 2009 (U.S. Department of Agriculture, February...
The U.S. Department of Agriculture defines a food desert as a census tract in which a...
The Economic Research Service of the U.S. Department of Agriculture has reported the results of a...
The U.S. Department of Agriculture is interested in analyzing the domestic market for soybean. The USDA’s...
1) A U.S. Department of Agriculture study of the demand for food products showed that the...
the farm security administration of u.s. department of agriculture a. encourages future farmers of America to...
The U.S. Department of Agriculture donates $125 million of rice to North Korea. This is recorded...
- Which of the following redox reactions do you expect to occur spontaneously in the reverse direction?...
- 2(a) A typical metallic particle has a rest mass (i.e. mass when the particle is not...
- In 500 words minimum: Evaluate when dividends are taxable, who they are taxable to, and the...
- 4. How might the researchers approach the measurement of validity? 5. What can the researchers do...
- Quick Answers. ty _____. 27. Environmental scanning is an important activity for an organization, it represents...
- The following tables form a Library database held in an RDBMS: Borrower (card_no , last_name ,...
- Create a html page to convert miles into kilometers, the page should have four buttons using...
 milcah answered 2 months ago
milcah answered 2 months ago