Question

Two 50 ?? long, thin parallel straight wires (grey) are connected at their ends by metal springs. The mass of each thin wire is 1.0 ?. The upper wire is connected to the ceiling by (non-conducting) stiff rods. Each spring has an equilibrium length of 5.0 ?? and a spring constant of ? = 0.50 ?/?. A steady current ? runs clockwise through the wire-spring loop as indicated by the arrow. At equilibrium, the lower rod hangs at a level 6.0 ?? below the upper wire. Find the magnitude of the current. You may ignore the magnetic fields generated by the springs, and you may approximate the magnetic fields generated by the wires as those from long, straight wires

Answer 1

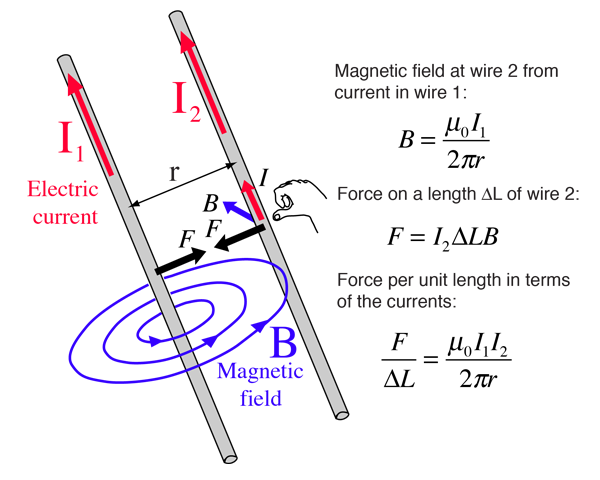
As you can see above if two parallel wires carry current in same direction they attract each other but in our case, they are in opposite directions Hence they repel.

The forces acting are

Magnetic repulsion will act downwards

Weight will act downwards

spring force will act upwards (wire is held)

Balancing them

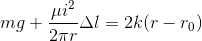
Here r0 is natural length of spring and r is given as 6cm.

m = 1gram dl = 50cm

Thus calculating individually

mg = 0.0098 N

2k(r-r0) = 2k(1cm) = 0.01N

Thus leaving us magnetic force = 2k(r-r0) - mg= 0.0002N

mu/2pi = 2 * 10^-7

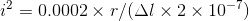
Thus

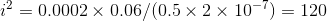
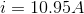
Please Upvote if you like the answer...