Suppose the expenditure function is e(p, u) = p1 * p2 + 2p1^1/2 * p2^ 1/2...

Suppose the expenditure function is e(p, u) = p1 * p2 + 2p1^1/2 * p2^ 1/2 * u. Then ∂e/∂p1 (p, u) = p2 + (p2/p1)^1/2*u and ∂e/∂p2(p, u) = p1 + (p1/p2)^1/2*u

(a) Find the Hicksian demand function h(p, u).
(b) Find the indirect utility function v(p,w) (this should be a function of w, p1, and p2).
(c) Find the demand function x(p, w). Are goods 1 and 2 substitutes or complements?

Expert Solution

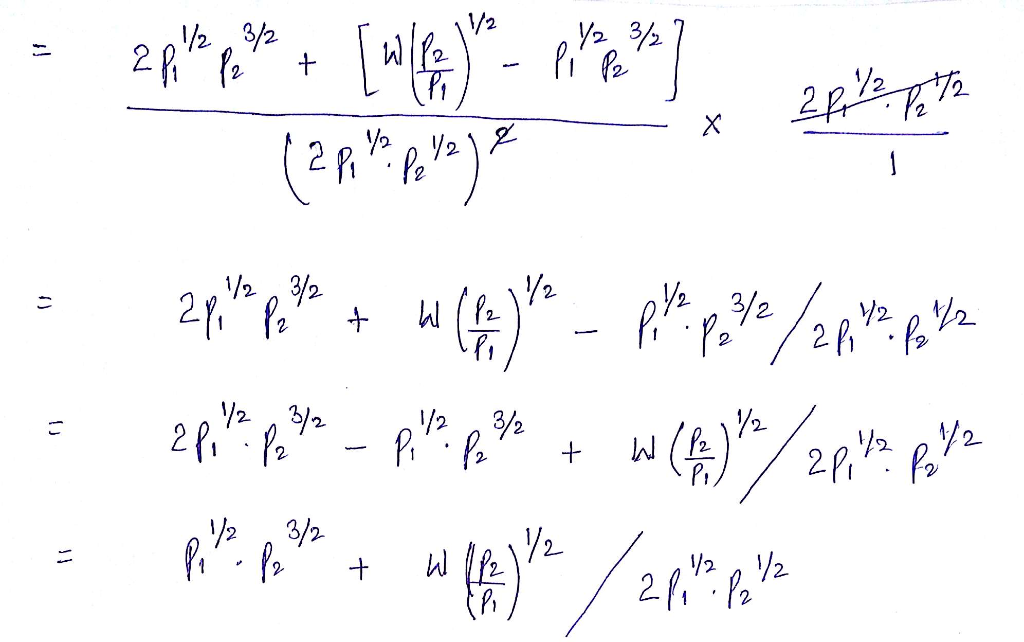
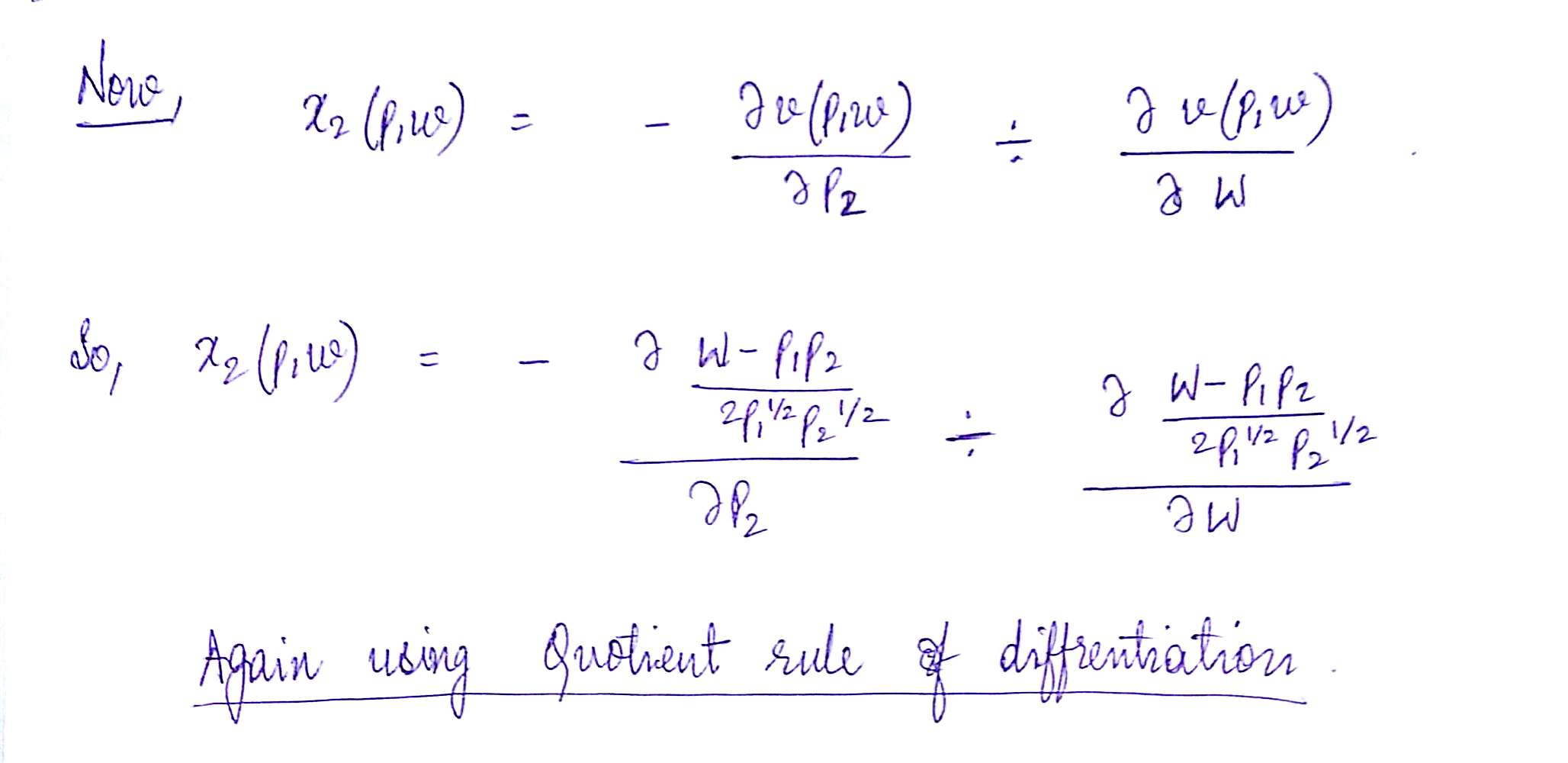
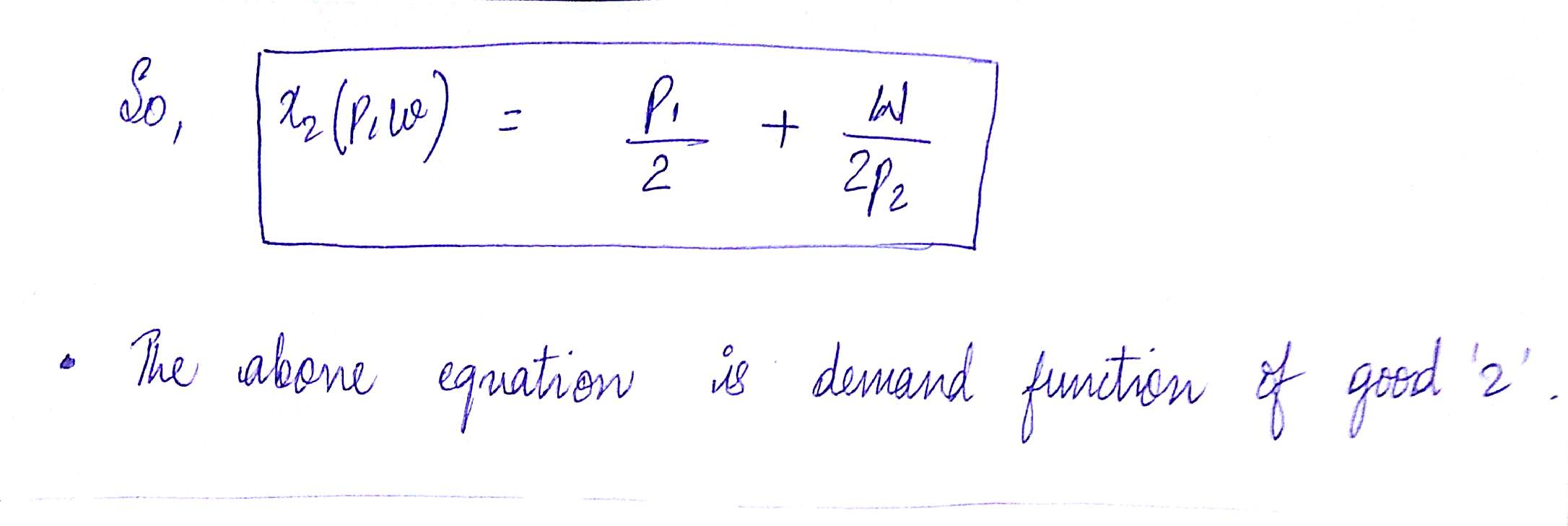Now demand function of goods 1 and 2 are :-

So, From Demand of x₁, we can see that as p₂ rises then x₁ will rise hence both goods are substitutes.

Similarly, From Demand of x₂ , we can see that as p₁ rises then x₂ rises hence both goods are substitutes.

So both the demand confirms that both goods are Substitutes.

Rahul Sunny answered 5 hours ago

Suppose an individual’s utility function is u = x11/2x21/2. Let p1=4, p2=5, and income equal $200....

Suppose an individual’s utility function is u = x11/2x21/2. Let p1=4, p2=5, and income equal $200. a. With a general equation and general prices, derive the equal marginal principle. Graphically illustrate equilibrium and disequilibrium conditions and how consumers can reallocate their consumption to maximize utility. b. What is the optimal amount of x1 consumed? c. What is the optimal amount of x2 consumed? d. What is the marginal rate of substitution at the optimal amounts of x1 and x2? e....

Construct a confidence interval for p 1 minus p 2p1−p2 at the given level of confidence....

Construct a confidence interval for p 1 minus p 2p1−p2 at the given level of confidence. x1=357, n1=502, x2=427427, n2=579, 99% confidence

Construct a confidence interval for p 1 minus p 2 p1−p2 at the given level of...

Construct a confidence interval for p 1 minus p 2 p1−p2 at the given level of confidence. x 1 equals x1= 375 375, n 1 equals n1= 523 523, x 2 equals x2= 432 432, n 2 equals n2= 585 585, 95 95% confidence The researchers are nothing % confident the difference between the two population proportions, p 1 minus p 2 p1−p2, is between nothing and nothing . (Use ascending order. Type an integer or decimal rounded to three...

Let pi = P(X = i) and suppose that p1 + p2 + p3 + p4...

Let pi = P(X = i) and suppose that p1 + p2 + p3 + p4 = 1. Suppose that E(X) = 2.5. (a) What values of p1, p2, p3, and p4 maximize Var(X)? (b) What values of p1, p2, p3, and p4 minimize Var(X)?

1. Consider this hypothesis test: H0: p1 - p2 = < 0 Ha: p1 - p2...

1. Consider this hypothesis test: H0: p1 - p2 = < 0 Ha: p1 - p2 > 0 Here p1 is the population proportion of “happy” of Population 1 and p2 is the population proportion of “happy” of Population 2. Use the statistics data from a simple random sample of each of the two populations to complete the following: Population 1 Population 2 Sample Size (n) 1000 1000 Number of “yes” 600 280 a. Compute the test statistic z. b....

k1 = k2 m1=9m^2 P1=P2 What is the relationship between P1 and P2? The momentum will...

k1 = k2 m1=9m^2 P1=P2 What is the relationship between P1 and P2? The momentum will be the same? K represents kinetic energy

Burt’s utility function is U(x1, x2)= min{x1,x2}. Suppose the price of good 1 is p1, the...

Burt’s utility function is U(x1, x2)= min{x1,x2}. Suppose the price of good 1 is p1, the price of good p2, the income is y. a. Derive ordinary demand functions. b. Draw indifference curves and budget line for the case when the price of good 1 is 10, the price of good 2 is 20, the income is 1200. c. Find the optimal consumption bundle.

10. Given the demand function of good 1: Q1=200-5P1+(P2)^2 Q1: the demand for good 1 P1:...

10. Given the demand function of good 1: Q1=200-5P1+(P2)^2 Q1: the demand for good 1 P1: the price for good 1 P2: the price of good 2 Answer the following questions What is the inverse demand function of good 1? Derive the expression of total revenue in terms of quantity of good 1(Q1) and price of good 2(P2). If total cost function C(Q1) = 30+(Q1)^2 , derive the profit function in terms of quantity of good 1(Q1) and price of...

The point Q (ql , q2) is the image of the point P(p1, P2) on the...

The point Q (ql , q2) is the image of the point P(p1, P2) on the line r . (ai + bj) + c = O. Show that a(q2 - P2) - b(qt - PI) = 0, a(p1 + ql) + b(P2 + q2) + 2c = O. Hence, express the coordinates of Q in terms of Pl, P2, a, b, c and find the coordinates of the image of the point (3,1) in the line r · (i +...

Write a function collision(p1, start1, p2, start2) that takes p1 and start1 of one vehicle, and...

Write a function collision(p1, start1, p2, start2) that takes p1 and start1 of one vehicle, and p2 and start2 of another vehicle, and checks whether the two vehicles will collide (i.e., at some stage they will be in the same cell at the same time). The function should return a tuple containing the (x,y) coordinates of the cell where they collide or None if they do not ever collide. If the two vehicles collide in multiple cells, return the coordinates...

Question