Question

The independaence postmaster suspects that working on ziptronic machines is the cause of high absenteeism. More than 10 absences from work without business related reason is considered excessive absenteeism. A check of employee recoreds shows that 26 of the 44 ziptronic operators had 10 or more absences and 35 of 120 nonziptronic workers had 10 or more absences. Construct a contingency table for the postmaster. Does the table support the postmaster’s suspicion that working on ziptronic machines is related to high absenteeism?

Answer 1

(a)Observed Frequencies:

	Ziptronic operators	Non-ziptronic operators	Totl
Absentees	26	35	61
Non-absentees	18	85	103
Total	44	120	164

H0: Working on ziptronic machine is not related to high absenteeism.

HA: Working on ziptronic machine is related to high absenteeism.

Assuming H0, the expected Frequencies are calculated as follows:

Expected Frequencies:

Observed Frequencies:

	Ziptronic operators	Non-ziptronic operators	Totl
Absentees	44X61/164=16.37	44.63	61
Non-absentees	27.63	75.37	103
Total	44	120	164

From the above Table, 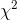Table is formed as follows:

O	E	(O - E)2/E
26	16.37	5.67
35	44.63	2.08
18	27.63	3.36
85	75.37	1.23
Total = 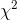=		12.34

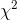= 12.34

ndf= (2 - 1) X (2 - 1) = 1

By Technology, p - value = 0.0004

Since p - value= 0.0004 is less than = 0.05, the difference is significant. Reject null hypothesis.

Conclusion:

The Table supports the postmaster's suspicion that working on ziptronic machines is related to high abserteeism.