Question

In: Math

The distribution of results from a cholesterol test has a mean of 180 and a standard...

The distribution of results from a cholesterol test has a mean of 180 and a standard deviation of 20. A sample size of 40 is drawn randomly.

Find the probability that the sum of the 40 values is less than 6,950.

Solutions

Expert Solution

Solution :

Given that,

mean = 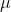= 180

standard deviation = 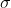= 20

n = 40

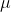
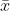= 180

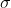
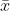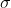= / n = 20 40 = 3.1623

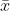  = (x / n)

= 6950 / 40

= 173.75

P(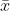 < 173.75 )

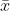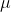
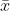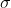
P ( - /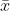) < ( 173.75 - 180 / 3.1623)

P ( z < -6.25 / 3.1623 )

P ( z < - 1.98 )

= 0.0239

Probability = 0.0239

milcah answered 2 days ago
Next > < Previous

Related Solutions

The distribution of results from a cholesterol test has a mean of 180 and a standard...
The distribution of results from a cholesterol test has a mean of 180 and a standard deviation of 20. A sample size of 40 is drawn randomly. a. Find the probability that the sum of the 40 values is greater than 7,500. b. Find the probability that the sum of the 40 values is less than 7,000. c. Find the sum that is one standard deviation above the mean of the sums. d. Find the sum that is 1.5 standard...
The distribution of results from a cholesterol test has a mean of 180 and a standard...
The distribution of results from a cholesterol test has a mean of 180 and a standard deviation of 20. A sample size of 40 is drawn randomly. Find the probability that the sum of the 40 values is greater than 7,450. (Round your answer to four decimal places.)
3. The distribution of results from a cholesterol test has a mean of 180 and a...
3. The distribution of results from a cholesterol test has a mean of 180 and a standard deviation of 20. A sample size of 40 is drawn randomly. a. Find the probability that the sum of the 40 values is greater than 7,550. (Round your answer to four decimal places. b. Find the sum that is 1.6 standard deviations below the mean of the sums. (Round your answer to two decimal places.) 4. A researcher measures the amount of sugar...
The distribution of results from a cholesterol test has a mean of 180 and a standard deviation of 20. A sample size of 40 is drawn randomly.
The distribution of results from a cholesterol test has a mean of 180 and a standard deviation of 20. A sample size of 40 is drawn randomly.Find the sum that is one standard deviation below the mean of the sums. (Round your answer to two decimal places.)
12. A standard IQ test has a normal distribution with a mean of 100 with a...
12. A standard IQ test has a normal distribution with a mean of 100 with a standard deviation of 15. a) A score of 145 or higher on this exam is categorized in the gifted realm. What percent of people would be considered gifted? ___________ b) The people who score in the lowest 5% of the standard IQ test are considered to have “mental retardation”. What cutoff score is used to qualify for this benchmark? ___________
A population has a mean of 180 and a standard deviation of 36. A sample of...
A population has a mean of 180 and a standard deviation of 36. A sample of 84 observations will be taken. The probability that the sample mean will be between 181 and 185 is
A population has a mean of 180 and a standard deviation of 24. A sample of...
A population has a mean of 180 and a standard deviation of 24. A sample of 64 observations will be taken. The probability that the sample mean will be between 183 and 186 is
A population has a mean of 180 and a standard deviation of 24. A sample of...
A population has a mean of 180 and a standard deviation of 24. A sample of 64 observations will be taken. The probability that the sample mean will be within 3 of the population mean is:
A population has a mean of 180 and a standard deviation of 24. A sample of...
A population has a mean of 180 and a standard deviation of 24. A sample of 64 observations will be taken. The probability that the sample mean will be less than or equal to 186 is
The distribution of certain test scores is a nonstandard normal distribution with a mean of 50 and a standard deviation of 6
The distribution of certain test scores is a nonstandard normal distribution with a mean of 50 and a standard deviation of 6. What are the values of the mean and standard deviation after all test scores have been standardized by converting them to z-scores using z = (x - µ) / σ ?Select one:a. The mean is 1 and the standard deviation is 0.b. The mean is 0 and the standard deviation is 1.c. The mean is 100 and the...
ADVERTISEMENT
Subjects
ADVERTISEMENT
Latest Questions
ADVERTISEMENT