If the momentum of a particle is doubled, what happens to its de Broglie wavelength? it...

If the momentum of a particle is doubled, what happens to its de Broglie wavelength?

it decreases by a factor of 2^-1/2

it doubles

it halves

it becomes slightly less than half

it slightly more than doubles

Solutions

Expert Solution

Ans: it halves

Because According to formula of de Broglie wavelength - wavelength is inversly proportional to momentum.

In some situations, light behaves like a wave, while in others, it behaves like particles. The particles of light are called photons, and they can be thought of as both waves and particles. Louis de Broglie developed a formula to relate this dual wave and particle behavior. It can also be applied to other particles, like electrons and protons. The formula relates the wavelength to the momentum of a wave/particle.

For particles with mass (electrons, protons, etc., but not photons), there is another form of the de Broglie wavelength formula. At non-relativistic speeds, the momentum of a particle is equal to its rest mass, m, multiplied by its velocity, v.

The unit of the de Broglie wavelength is meters (m), though it is often very small, and so expressed in nanometers (1 nm = 10^(-9) m), or Angstroms ().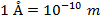

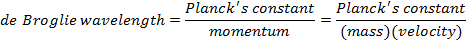
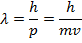
λ = the de Broglie wavelength (m)

h = Planck's constant ()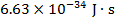

p = momentum of a particle ()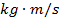

m = mass of a particle (kg)

v = velocity of a particle (m/s)

genius_generous answered 1 week ago

Next > < Previous

Related Solutions

The de Broglie wavelength of a proton in a particle accelerator is 1.81 × 10-14 m....

The de Broglie wavelength of a proton in a particle accelerator is 1.81 × 10-14 m. Determine the kinetic energy (in joules) of the proton.

1. For what kinetic energy is the de Broglie wavelength of an electron equal to its...

1. For what kinetic energy is the de Broglie wavelength of an electron equal to its Compton wavelength? Express your answer in units of mc2 in doing the calculation, and then use mc2 = 0.5 MeV.(Answer: 0.2 MeV) 2. A beam of electrons with energy 1.0 eV approaches a potential barrier with U = 2.0 eV, whose width is 0.10 nm (see a figure below). Estimate the fraction of electrons that tunnel through the barrier. (Hint: use the relation of...

An electron has a de Broglie wavelength of 235 nm .What is the speed of the...

An electron has a de Broglie wavelength of 235 nm .What is the speed of the electron? --------------------------------------------------------------------- How much energy is contained in 1 mol of γ-ray photons with a wavelength of 2.43×10−5 nm . ? ------------------------------------------------------------------------ In a technique used for surface analysis called auger electron spectroscopy (AES), electrons are accelerated toward a metal surface. These electrons cause the emissions of secondary electrons-called auger electrons-from the metal surface. The kinetic energy of the auger electrons depends on the...

a) Derive an expression for the de Broglie wavelength of an electron in the Bohr model...

a) Derive an expression for the de Broglie wavelength of an electron in the Bohr model of the hydrogen atom as a function of a0 and n. b) Assume the uncertainty of the electron’s position is the diameter of its Bohr orbit. Derive an expression for the minimum uncertainty in electron’s velocity, (∆vn) as function of a0 and n (and other constants). c) Use quantization of angular momentum to write an expression for the velocity as a function of n,...

Explain what physicists mean when they say that the de Broglie wavelength relates to the probability...

Explain what physicists mean when they say that the de Broglie wavelength relates to the probability distribution wave function. Please be specific and do not copy and paste previous answers.

In this example we will apply the concept of the de Broglie wavelength to neutrons. Find...

In this example we will apply the concept of the de Broglie wavelength to neutrons. Find the speed and kinetic energy of a neutron (m=1.675×10−27kg)(m=1.675×10−27kg) that has a de Broglie wavelength λ=0.200nmλ=0.200nm, typical of atomic spacing in crystals. Compare the energy with the average kinetic energy of a gas molecule at room temperature (T=20∘C)(T=20∘C). Find the kinetic energy of an electron with a de Broglie wavelength of 0.163 nmnm .

Question