Question
In: Physics
A block of wood of mass 4 kg is connected to a spring, whose other end...
A block of wood of mass 4 kg is connected to a spring, whose other end is tethered to a wall. As the spring is stretched and compressed, the block undergoes simple harmonic motion on the (frictionless) floor. The displacement of the block with respect to its equilibrium position is x = 0.205 cos ( 22.5 t ) where x is measured in m and t is measured in seconds.
1.) Which of these statements is true at time t = 0 ?
choice (a)Both kinetic and potential energy are maximum
choice (B) The potential energy is maximum and the kinetic energy is zero Both kinetic and potential energy are zero
chioce (c) The kinetic energy is maximum and the potential energy is zero
2.) For t > 0 , when is the first time when the kinetic and the potential energies are both exactly what they were at t = 0 ? which statement
choice (a) t = 0.13964444444444 s
(b) t = 0.069822222222222 s
(c) t = 0.27928888888889 s
3.) What is the total energy of the system?
Solutions
Expert Solution
Diagramatic representation of the problem
We have
- Displacement,
- Potential Energy,
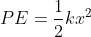 where k is spring constant
where k is spring constant - Kinetic Energy,
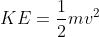 where m is the mass of wood block and v is the velocity of wood
block;
where m is the mass of wood block and v is the velocity of wood
block; 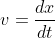 where dx is change in displacement and dt is change in time.
where dx is change in displacement and dt is change in time.
- At t = 0, The potential energy is maximum and the kinetic energy is zero (Since cos(0) = 1; x = 0.205 is the maximum displacement.)
- The first time when the kinetic and the potential energies are both exactly what they were at t = 0 is when the spring compresses after the maximum displacement.
i.e., x = - 0.205


 ;
;


3. The total energy of the system is

Related Solutions
a) A block with a mass of 0.600 kg is connected to a spring, displaced in...
The displacement of a block of mass 1.280 kg attached to a spring whose spring constant...
A block of mass 1.59 kg is connected to a spring of spring constant 148 N/m...
A block with mass M is connected to one end of a horizontal spring of constant...
A block with a mass m = 2.12 kg is pushed into an ideal spring whose...
A block with mass 5 kg is attached to the end of a horizontal spring with...
the figure, block 2 of mass 2.20 kg oscillates on the end of a spring in...
In the figure, block 2 of mass 2.90 kg oscillates on the end of a spring...
A 23.3-kg mass is attached to one end of a horizontal spring, with the other end of the spring fixed to a wall.
a block of mass m=0.10 kg attached to a spring whose spring constant is k=2.5 N/m...
- MINIMUM MAIN.CPP CODE /******************************** * Week 4 lesson: * * finding the smallest number * *********************************/...
- Do you think President Eisenhower had a successful presidency?
- Barbour Corporation, located in Buffalo, New York, is a retailer of high-tech products and is known...
- C PROGRAMMIMG I want to check if my 2 input is a number or not all...
- In long paragraphs answer the questions below: Discuss the key components (where, when, what) and causes...
- Sinkal Co. was formed on January 1, 2018 as a wholly owned foreign subsidiary of a...
- Larry’s best friend, Garfield, owns a lasagna factory. Garfield’s financial skills are not very strong, so...
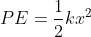 where k is spring constant
where k is spring constant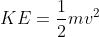 where m is the mass of wood block and v is the velocity of wood
block;
where m is the mass of wood block and v is the velocity of wood
block; 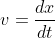 where dx is change in displacement and dt is change in time.
where dx is change in displacement and dt is change in time. genius_generous answered 3 years ago
genius_generous answered 3 years ago