Question

What quantities determine how quickly a wave travels along a string? Choose all that apply..

a)Mass of the string

b)Length of the string

c)Tension in the string

d)Linear density of the string

Answer 1

The properties of the material* or medium through which a wave travels determine the speed of the wave. For example, Figure shows a transverse wave on a string and draws attention to four string particles that have been drawn as colored dots. As the wave moves to the right, each particle is displaced, one after the other, from its undisturbed position. In the drawing, particles 1 and 2 have already been displaced upward, while particles 3 and 4 are not yet affected by the wave. Particle 3 will be next to move because the section of string immediately to its left (i.e., particle 2) will pull it upward.

Figure As a transverse wave moves to the right with speed v, each string particle is displaced, one after the other, from its undisturbed position.

Figure leads us to conclude that the speed with which the wave moves to the right depends on how quickly one particle of the string is accelerated upward in response to the net pulling force exerted by its adjacent neighbors. In accord with Newton’s second law, a stronger net force results in a greater acceleration, and, thus, a faster-moving wave. The ability of one particle to pull on its neighbors depends on how tightly the string is stretched—that is, on the tension. The greater the tension, the greater the pulling force the particles exert on each other, and the faster the wave travels, other things being equal. Along with the tension, a second factor influences the wave speed. According to Newton’s second law, the inertia or mass of particle 3 in Figure also affects how quickly it responds to the upward pull of particle 2. For a given net pulling force, a smaller mass has a greater acceleration than a larger mass. Therefore, other things being equal, a wave travels faster on a string whose particles have a small mass, or, as it turns out, on a string that has a small mass per unit length. The mass per unit length is called the linear density of the string. It is the mass m of the string divided by its length L, or m/L. The effects of the tension F and the mass per unit length are evident in the following expression for the speed v of a small-amplitude wave on a string:

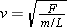So, Answer will be-

c)Tension in the string

d)Linear density of the string But, if that doesn't work than you can choose all the four because linear density depends on mass and length also, which means speed depends on mass and length also, but more accurately it depends on linear density.