Question

1. explain why ia an ohmic the current through the resistor is proportional to the voltage differnce across the resistor. your explanation must refer to the electric field

Answer 1

Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points. Introducing the constant of proportionality, the resistance,^[1] one arrives at the usual mathematical equation that describes this relationship:^[2]

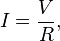
where I is the current through the conductor in units of amperes, V is the potential difference measured across the conductor in units of volts, and Ris the resistance of the conductor in units of ohms. More specifically, Ohm's law states that the R in this relation is constant, independent of the current.^[3]

The law was named after the German physicist Georg Ohm, who, in a treatise published in 1827, described measurements of applied voltage and current through simple electrical circuits containing various lengths of wire. He presented a slightly more complex equation than the one above (seeHistory section below) to explain his experimental results. The above equation is the modern form of Ohm's law.

In physics, the term Ohm's law is also used to refer to various generalizations of the law originally formulated by Ohm. The simplest example of this is:

where J is the current density at a given location in a resistive material, E is the electric field at that location, and ? (Sigma) is a material dependent parameter called the conductivity. This reformulation of Ohm's law is due to Gustav Kirchhoff.

Circuit analysis

Ohm's law triangle

In circuit analysis, three equivalent expressions of Ohm's law are used interchangeably:

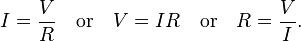
Each equation is quoted by some sources as the defining relationship of Ohm's law,^[2][20][21] or all three are quoted,^[22] or derived from a proportional form,^[23] or even just the two that do not correspond to Ohm's original statement may sometimes be given.^[24][25]

The interchangeability of the equation may be represented by a triangle, where V (voltage) is placed on the top section, the I (current) is placed to the left section, and the R (resistance) is placed to the right. The line that divides the left and right sections indicate multiplication, and the divider between the top and bottom sections indicates division (hence the division bar).