Question
In: Statistics and Probability
Explain the concept of statistical power. Briefly explain how power is calculated and what information you...
Explain the concept of statistical power. Briefly explain how power is calculated and what information you might have to assume or know in order to make this calculation.
Solutions
Expert Solution
The power of any test of statistical significance is defined as the probability that it will reject a false null hypothesis. Statistical power is inversely related to betaor the probability of making a Type II error. In short, power = 1 – β.
Factors That Affect Power
The power of a hypothesis test is affected by three factors.
- Sample size (n). Other things being equal, the greater the sample size, the greater the power of the test.
- Significance level (α). The lower the significance level, the lower the power of the test. If you reduce the significance level (e.g., from 0.05 to 0.01), theregion of acceptance gets bigger. As a result, you are less likely to reject the null hypothesis. This means you are less likely to reject the null hypothesis when it is false, so you are more likely to make a Type II error. In short, the power of the test is reduced when you reduce the significance level; and vice versa.
- The "true" value of the parameter being tested. The greater the difference between the "true" value of a parameter and the value specified in the null hypothesis, the greater the power of the test. That is, the greater the effect size, the greater the power of the test.
Suppose a child psychologist says that the average time that working mothers spend talking to their children is 11 minutes per day. You want to test

versus

Toggle navigation
- EDUCATION
- MATH
- STATISTICS
- FINDING THE POWER OF A HYPOTHESIS TEST
FINDING THE POWER OF A HYPOTHESIS TEST

RELATED BOOK
U Can: Statistics For Dummies
By Deborah J. Rumsey, David Unger
When you make a decision in a hypothesis test, there’s never a 100 percent guarantee you’re right. You must be cautious of Type I errors (rejecting a true claim) and Type II errors (failing to reject a false claim). Instead, you hope that your procedures and data are good enough to properly reject a false claim.
The probability of correctly rejecting H0when it is false is known as the power of the test. The larger it is, the better.
Suppose you want to calculate the power of a hypothesis test on a population mean when the standard deviation is known. Before calculating the power of a test, you need the following:
-
The previously claimed value of
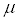
in the null hypothesis,
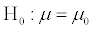
-
The one-sided inequality of the alternative hypothesis (either < or >), for example,
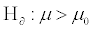
-
The mean of the observed values
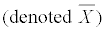
-
The population standard deviation
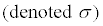
-
The sample size (denoted n)
-
The level of significance
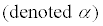
To calculate power, you basically work two problems back-to-back. First, find a percentile assuming that H0 is true. Then, turn it around and find the probability that you’d get that value assuming H0 is false (and instead Ha is true).
-
Assume that H0 is true, and
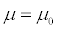
-
Find the percentile value corresponding to
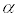
sitting in the tail(s) corresponding to Ha. That is, if
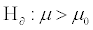
then find b where
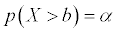
If
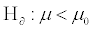
then find b where
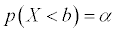
-
Assume that H0 is false, and instead Ha is true. Since
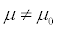
under this assumption, then let

in the next step.
-
Find the power by calculating the probability of getting a value more extreme than b from Step 2 in the direction of Ha. This process is similar to finding the p-value in a test of a single population mean, but instead of using
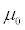
you use

Suppose a child psychologist says that the average time that working mothers spend talking to their children is 11 minutes per day. You want to test

versus

You conduct a random sample of 100 working mothers and find they spend an average of 11.5 minutes per day talking with their children. Assume prior research suggests the population standard deviation is 2.3 minutes.
When conducting this hypothesis test for a population mean, you find that the p-value = 0.015, and with a level of significance of

you reject the null hypothesis. But there are a lot of different values of

(not just 11.5) that would lead you to reject H0. So how strong is this specific test? Find the power.
-
Assume that H0 is true, and
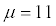
-
Find the percentile value corresponding to
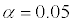
sitting in the upper tail. If p(Z > zb) = 0.05, then zb = 1.645. Further,

-
Assume that H0 is false, and instead
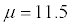
-
Find the power by calculating the probability of getting a value more extreme than b from Step 2 in the direction of Ha. Here, you need to find p(Z> z) where
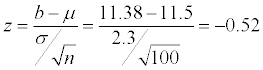
Using the Z-table, you find that
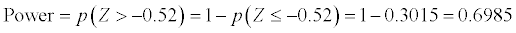
Related Solutions
Define the concept of statistical process control Explain briefly the rationale for SPC What is meant...
Explain the concept of Bond Duration, what does it measure, how is it calculated, how is...
Briefly explain what you understand by Earnings per share (EPS). How is EPS calculated and why...
Briefly explain the concept of the indeterminacy of labor power in labor process theory.
Explain the concept if sample power. How is sample power related to hypotgesis testing? how is...
Explain the concept of “statistical learning” and why it is important. How does it relate to...
Explain in your own words the “power of a statistical test”. Do you proceed with the...
Discuss how the concept of statistical independence underlies statistical hypothesis testing in general. Based on statistical...
Discuss how the concept of statistical independence underlies statistical hypothesis testing in general. Based on statistical...
Briefly explain how the calculated molar mass of HCL would be affected if the HCL saturated...
- define the following functional plans MBO mission
- I am new to python, and i used python 3. i have to make a new...
- The December 31, 20X8, balance sheets for Pint Corporation and its 70 percent-owned subsidiary Saloon Company...
- plot this data into a bar graph: PYTHON data=pandas.read_csv(r'data/tv_shows.txt', low_memory=False) print((data)) print((data.columns)) TV Shows : Rating...
- At 25 degrees celsius only .0640 mol of the generic salt AB2 is soluble in 1.00...
- cite 3 most important healthcare financing concern in the united states today and how expenses and...
- S Company reported the following account balances on its After Closing Trial Balance
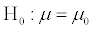
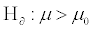
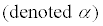
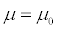
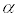
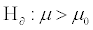
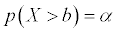
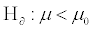
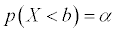
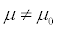

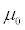

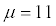
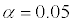

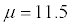
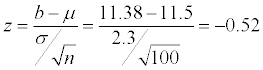
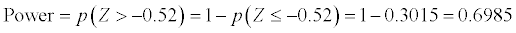
 orchestra answered 3 years ago
orchestra answered 3 years ago