Question

Please show how calculus can be used in respect to measuring the change of current or wave over a circuit. Please explain how the problem works and what is happening at each step.

Answer 1

In general an electrical circuit can have resistances, inductors and capacitors. Consider the following circuit.

In this circuit, the three components are all in series with the voltage source. The governing differential equation can be found by substituting into Kirchhoff's voltage law (KVL) the constitutive equation for each of the three elements. From KVL,

where are the voltages across R, L and C respectively and is the time varying voltage from the source. Substituting in the constitutive equations,

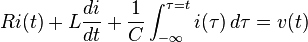
For the case where the source is an unchanging voltage, differentiating and dividing by L leads to the second order differential equation:

This can usefully be expressed in a more generally applicable form:

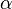and are both in units of angular frequency. 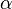is called the neper frequency, or attenuation, and is a measure of how fast the transient response of the circuit will die away after the stimulus has been removed.

The differential equation for the circuit solves in three different ways depending on the value of . These are underdamped (), overdamped () and critically damped (). The differential equation has the characteristic equation,

The roots of the equation in s are,

The general solution of the differential equation is an exponential in either root or a linear superposition of both,

The coefficients A₁ and A₂ are determined by the boundary conditions of the specific problem being analysed. That is, they are set by the values of the currents and voltages in the circuit at the onset of the transient and the presumed value they will settle to after infinite time.

Overdamped response

The overdamped response () is,

The overdamped response is a decay of the transient current without oscillation.

Underdamped response

The underdamped response () is,

By applying standard trigonometric identities the two trigonometric functions may be expressed as a single sinusoid with phase shift,

The underdamped response is a decaying oscillation at frequency . The oscillation decays at a rate determined by the attenuation 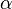. The exponential in 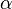describes the envelope of the oscillation. B₁ and B₂ (or B₃ and the phase shift 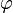in the second form) are arbitrary constants determined by boundary conditions. The frequency is given by,

This is called the damped resonance frequency or the damped natural frequency. It is the frequency the circuit will naturally oscillate at if not driven by an external source. The resonance frequency, , which is the frequency at which the circuit will resonate when driven by an external oscillation, may often be referred to as the undamped resonance frequency to distinguish it.

Critically damped response

The critically damped response () is,

The critically damped response represents the circuit response that decays in the fastest possible time without going into oscillation. This consideration is important in control systems where it is required to reach the desired state as quickly as possible without overshooting. D₁ and D₂ are arbitrary constants determined by boundary conditions.