Question

Define a relation S from R to R by saying that  if and only if

(a) List five different elements of S.
(b) Prove that S is not a function.

Answer 1

Equivalence Relation Definition

A relation R on a set A is said to be an equivalence relation if and only if the relation R is reflexive, symmetric and transitive.

Reflexive: A relation is said to be reflexive, if (a, a) ∈ R, for every a ∈ A.

Symmetric: A relation is said to be symmetric, if (a, b) ∈ R, then (b, a) ∈ R.

Transitive: A relation is said to be transitive if (a, b) ∈ R and (b, c) ∈ R, then (a, c) ∈ R.

Equivalence relations can be explained in terms of the following examples:

• The sign of ‘is equal to’ on a set of numbers; for example, 1/3 is equal to 3/9.
• For a given set of triangles, the relation of ‘is similar to’ and ‘is congruent to’.
• For a given set of integers, the relation of ‘is congruent to, modulo n’ shows equivalence.
• The image and domain are the same under a function, shows the relation of equivalence.
• For a set of all angles, ‘has the same cosine’.
• For a set of all real numbers,’ has the same absolute value.

  Relations Definition

  A relation in mathematics defines the relationship between two different sets of information. If two sets are considered, the relation between them will be established if there is a connection between the elements of two or more non-empty sets.

  In the morning assembly at schools, students are supposed to stand in a queue in ascending order of the heights of all the students. This defines an ordered relation between the students and their heights.

  Therefore, we can say,

  ‘A set of ordered pairs is defined as a relation.’

  

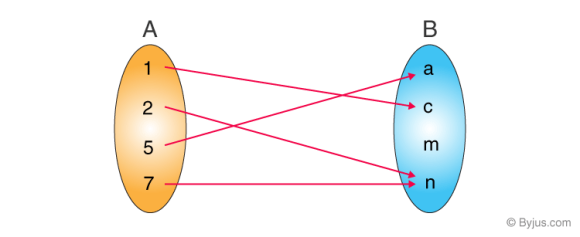
  This mapping depicts a relation from set A into set B. A relation from A to B is a subset of A x B. The ordered pairs are (1,c),(2,n),(5,a),(7,n). For defining a relation, we use the notation where,

  set {1, 2, 5, 7} represents the domain.

  set {a, c, n} represents the range.

  Sets and Relations

  Sets and relation are interconnected with each other. The relation defines the relation between two given sets.

  If there are two sets available, then to check if there is any connection between the two sets, we use relations.

  For example, An empty relation denotes none of the elements in the two sets is same.

  Let us discuss the other types of relations here.

  Relations in Mathematics

  In Maths, the relation is the relationship between two or more set of values.
  Suppose, x and y are two sets of ordered pairs. And set x has relation with set y, then the values of set x are called domain whereas the values of set y are called range.
  Example: For ordered pairs={(1,2),(-3,4),(5,6),(-7,8),(9,2)}
  The domain is = {-7,-3,1,5,9}
  And range is = {2,4,6,8}

  Types of Relations

  There are 8 main types of relations which include:

• Empty Relation
• Universal Relation
• Identity Relation
• Inverse Relation
• Reflexive Relation
• Symmetric Relation
• Transitive Relation
• Equivalence Relation

• Empty Relation

  An empty relation (or void relation) is one in which there is no relation between any elements of a set. For example, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where, |x – y| = 8. For empty relation,

  R = φ ⊂ A × A

  Universal Relation

  A universal (or full relation) is a type of relation in which every element of a set is related to each other. Consider set A = {a, b, c}. Now one of the universal relations will be R = {x, y} where, |x – y| ≥ 0. For universal relation,

  R = A × A

  Identity Relation

  In an identity relation, every element of a set is related to itself only. For example, in a set A = {a, b, c}, the identity relation will be I = {a, a}, {b, b}, {c, c}. For identity relation,

  I = {(a, a), a ∈ A}

  Inverse Relation

  Inverse relation is seen when a set has elements which are inverse pairs of another set. For example if set A = {(a, b), (c, d)}, then inverse relation will be R^-1 = {(b, a), (d, c)}. So, for an inverse relation,

  R^-1 = {(b, a): (a, b) ∈ R}

  Reflexive Relation

  In a reflexive relation, every element maps to itself. For example, consider a set A = {1, 2,}. Now an example of reflexive relation will be R = {(1, 1), (2, 2), (1, 2), (2, 1)}. The reflexive relation is given by-

  (a, a) ∈ R

  Symmetric Relation

  In a symmetric relation, if a=b is true then b=a is also true. In other words, a relation R is symmetric only if (b, a) ∈ R is true when (a,b) ∈ R. An example of symmetric relation will be R = {(1, 2), (2, 1)} for a set A = {1, 2}. So, for a symmetric relation,

  aRb ⇒ bRa, ∀ a, b ∈ A

  Transitive Relation

  For transitive relation, if (x, y) ∈ R, (y, z) ∈ R, then (x, z) ∈ R. For a transitive relation,

  aRb and bRc ⇒ aRc ∀ a, b, c ∈ A

  Equivalence Relation

  If a relation is reflexive, symmetric and transitive at the same time it is known as an equivalence relation.

  Representation of Types of Relations

  Relation Type	Condition
  Empty Relation	R = φ ⊂ A × A
  Universal Relation	R = A × A
  Identity Relation	I = {(a, a), a ∈ A}
  Inverse Relation	R-1 = {(b, a): (a, b) ∈ R}
  Reflexive Relation	(a, a) ∈ R
  Symmetric Relation	aRb ⇒ bRa, ∀ a, b ∈ A
  Transitive Relation	aRb and bRc ⇒ aRc ∀ a, b, c ∈ A

• Equal Sets

  Two sets X and Y are said to be equal if every element of set X is also the elements of set Y and if every element of set Y is also the elements of set X. It means set X and set Y have the same elements, and we can denote it as;

  X = Y

  For example, Let X = { 1, 2, 3, 4} and Y = {4, 3, 2, 1}, then X = Y

  And if X = {set of even numbers} and Y = { set of natural numbers} the X ≠ Y, because natural numbers consist of all the positive integers starting from 1, 2, 3, 4, 5 to infinity, but even numbers starts with 2, 4, 6, 8, and so on.

  Subsets

  A set X is said to be a subset of set Y if the elements of set X belongs to set Y, or you can say each element of set X is present in set Y. It is denoted with the symbol as X ⊂ Y.

  We can also write the subset notation as;

  X ⊂ Y if a ∊ X ⇒ a ∊ Y

  Thus, from the above equation, “X is a subset of Y if a is an element of X implies that a is also an element of Y”.

  Each set is a subset of its own set, and a null set or empty set is a subset of all sets.

  Power Sets

  The power set is nothing but the set of all subsets. Let us explain how.

  We know the empty set is a subset of all sets and every set is a subset of itself. Taking an example of set X = {2, 3}. From the above given statements we can write,

  {} is a subset of {2, 3}

  {2} is a subset of {2, 3}

  {3} is a subset of {2, 3}

  {2, 3} is also a subset of {2, 3}

  Therefore, power set of X = {2, 3},

  P(X) = {{},{2},{3},{2,3}}

  Universal Sets

  A universal set is a set which contains all the elements of other sets. Generally, it is represented as ‘U’.

  For example; set X = {1, 2, 3}, set Y = {3, 4, 5, 6} and Z = {5, 6, 7, 8, 9}

  Then, we can write universal set as, U = {1, 2, 3, 4, 5, 6, 7, 8, 9,}

  Note: From the definition of the universal set, we can say, all the sets are subsets of the universal set. Therefore,

  X ⊂ U

  Y ⊂ U

  And Z ⊂ U

  Union of sets

  A union of two sets has all their elements. It is denoted by ⋃.

  For example, set X = {2, 3, 7} and set Y = { 4, 5, 8}

  Then union of set X and set Y will be;

  X ⋃ Y = {2, 3, 7, 4, 5, 8}

  Properties of Union of Sets:

  X ⋃ Y = Y ⋃ X ; Commutative law

  (X ⋃ Y) ⋃ Z = X ⋃ (Y ⋃ Z)

  X ⋃ {} = X ; {} is the identity of ⋃

  X ⋃ X = X

  U ⋃ X = U

  Intersection of Sets

  Set of all elements, which are common to all the given sets, gives intersection of sets. It is denoted by the symbol ⋂.

  For example, set X = {2, 3, 7} and set Y = {2, 4, 9}

  So, X ⋂ Y = {2}

  Difference of Sets

  The difference of set X and set Y is such that, it has only those elements which are in the set X and not in the set Y.

  i.e. X – Y = {a: a ∊ X and a ∉ Y}

  In the same manner, Y – X = {a: a ∊ Y and a ∉ X}

  For example, if set X = {a, b, c, d} and Y = {b, c, e, f} then,

  X – Y = {a, d} and Y – X = {e, f}

  Disjoint Sets

  If two sets X and Y have no common elements, and their intersection results in zero(0), then set X and Y are called disjoint sets.

  It can be represented as; X ∩ Y = 0