Question

In: Math

5. The population of certain small organism grows according to the model: dy/dt = 5y where...

5. The population of certain small organism grows according to the model: dy/dt = 5y where y=20 when t=0

t is measured in months. a) Construct the specific function for y. b) Find how many in the population of this organism after 8 months. c) Determine how many months until there are 228 of this organism. Round to the nearest 0.1

Solutions

Expert Solution

PART(a):

The given DE is,

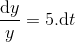
integrating on both sides,

where A is an integration const.

To find A, we have y(0) = 20,

Now the final solution becomes,

PART(b):

put t = 8,

PART(c):

put y(t) = 228,

rounding off to 1 decimal

I hope this answer helps,
Thanks,
Keep posting questions.

milcah answered 1 year ago

Next > < Previous

Related Solutions

Solve the system of equation by method of elimination. dx/dt + x−5y = 0, 4x +dy/dt+...

Solve the system of equation by method of elimination. dx/dt + x−5y = 0, 4x +dy/dt+ 5y = 0, x(0) = −1, y(0) = 2.

Use a LaPlace transform to solve d^2x/dt^2+dx/dt+dy/dt=0 d^2y/dt^2+dy/dt-4dy/dt=0 x(0)=1,x'(0)=0 y(0)=-1,y'(0)=5

Section 5.3: Find the equilibrium values of a general quadratic population model: dx/dt=a1x+b1x^2+c1xy dy/dt=a2y+b2y^2+c2xy Don’t forget...

Section 5.3: Find the equilibrium values of a general quadratic population model: dx/dt=a1x+b1x^2+c1xy dy/dt=a2y+b2y^2+c2xy Don’t forget to show this for all four cases: Case 1: ? = 0, ? = 0 Case 2: ? ≠ 0, ? = 0 Case 3: ? = 0, ? ≠ 0 Case 4: ? ≠ 0, ? ≠ 0 (Use Cramer’s Rule to set up the solution for this case.)

Solve by separation variables (2x-5y-2)dx+(5x-y-5)dy=0

In the Republic of Pecunia 1100 individuals are born in period t. The population grows according...

In the Republic of Pecunia 1100 individuals are born in period t. The population grows according to Nt = 1.1Nt−1. Each citizen in Pecunia is endowed with y1 = 15 units of the consumption good when young, and y2 = 5.5 units when old. Preferences are such that individuals will always want to consume more than their endowment when old. The fiat money stock in period t amounts to 2500. The Pecunian government is increasing the stock of fiat money...

STM 2100 Quiz April 2 2020 Consider the radioactive decay model dy/dt = -0.1y y(0) =...

STM 2100 Quiz April 2 2020 Consider the radioactive decay model dy/dt = -0.1y y(0) = 10 a. Use separation of variables to solve the ODE b. At what time does y(t) = 5? 2. Consider the logistic model given by the following ODE dy/dt = y(1-y) y(0) = 0.1 a. Use separation of variables to rewrite the problem as an equality of two integrals b. Use partial fractions to rewrite 1/y(1-y) as the sum of two fractions, each of...

According to Taylor, every "organism, species, population, and community of life has a good of its...

According to Taylor, every "organism, species, population, and community of life has a good of its own." What does he mean by that claim? What relevance does it have for environmental ethics,,,, in seven sentence.

Recall the moving average model dt = et − θet−1, where et are independent with mean...

Recall the moving average model dt = et − θet−1, where et are independent with mean 0 and variance σ2. Find its autocorrelation function ρk = Cor(dt,dt−k).

Classical small open economy model: According to the Classical small open economy model, what happens to...

Classical small open economy model: According to the Classical small open economy model, what happens to domestic national saving, investment, the trade balance, and the real exchange rate in response to each of the following events? Draw a loanable funds market diagram and a net exports diagram to illustrate your answer in each case. (For these diagrams, let’s assume that the country starts out running a current account surplus and capital account deficit, as in the examples in class.) a)...

According to a health organization in a certain? country, 19.6?% of the population smoked in 2008....

According to a health organization in a certain? country, 19.6?% of the population smoked in 2008. In? 2014, a random sample of 750 citizens of this country was? selected, 153 of whom smoked. Complete parts a through c below. a. Construct a 99?% confidence interval to estimate the actual proportion of people who smoked in this country in 2014. A 99?% confidence interval to estimate the actual proportion has a lower limit of nothing and an upper limit of nothing....

Subjects