Question

Using the definition of magnitude: m=-2.5log F + C derive the relation for the distance modulus: m-M=5logd-5

Answer 1

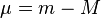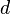The distance modulus is the difference between the apparent magnitude (ideally, corrected from the effects of interstellar absorption) and the absolute magnitude of an astronomical object. It is related to the distance in parsecs by:

This definition is convenient because the observed brightness of a light source is related to its distance by the inverse square law (a source twice as far away appears one quarter as bright) and because brightnesses are usually expressed not directly, but in magnitudes.

Absolute magnitude is defined as the apparent magnitude of an object when seen at a distance of 10 parsecs. Suppose a light source has luminosity L(d) when observed from a distance of 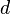parsecs, and luminosity L(10) when observed from a distance of 10 parsecs. The inverse-square law is then written like:

The magnitudes and luminosities are related by:

Substituting and rearranging, we get:

which means that the apparent magnitude is the absolute magnitude plus the distance modulus.

Isolating 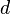from the equation , we find that the distance (or, the luminosity distance) in parsecs is given by

The uncertainty in the distance in parsecs (?d) can be computed from the uncertainty in the distance modulus (??) using

which is derived using standard error analysis.