Question

What is Generalised extreme value (GEV) and what is it used for give examples aswell

Answer 1

In probability theory and statistics, the generalized extreme value (GEV) distributionis a family of continuous probability distributions developed within extreme value theory to combine the Gumbel, Fréchet and Weibull families also known as type I, II and III extreme value distributions. By the extreme value theorem the GEV distribution is the only possible limit distribution of properly normalized maxima of a sequence of independent and identically distributed random variables. Note that a limit distribution need not exist: this requires regularity conditions on the tail of the distribution. Despite this, the GEV distribution is often used as an approximation to model the maxima of long (finite) sequences of random variables.

Notation	{\displaystyle {\textrm {GEV}}(\mu ,\,\sigma ,\,\xi )}

• The GEV distribution is widely used in the treatment of "tail risks" in fields ranging from insurance to finance. In the latter case, it has been considered as a means of assessing various financial risks via metrics such as Value at Risk.^[3][4]

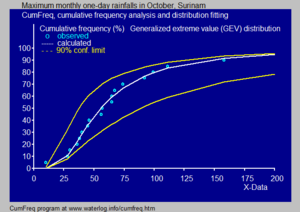
Fitted GEV probability distribution to monthly maximum one-day rainfalls in October, Surinam^[5]

• However, the resulting shape parameters have been found to lie in the range leading to undefined means and variances, which underlines the fact that reliable data analysis is often impossible.^[6]

• In hydrology the GEV distribution is applied to extreme events such as annual maximum one-day rainfalls and river discharges. The blue picture, made with CumFreq, illustrates an example of fitting the GEV distribution to ranked annually maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of the cumulative frequency analysis.