Question
In: Statistics and Probability
A group of 5 people are to be chosen from a collection of 12 people. Of...
Solutions
Expert Solution
Given
Total number of people = 12
Number of Democrats = 6
Number of Republicans = 4
Number of Independents = 2
Number of people to be chosen = 5
A)
The possible number of committes


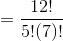
= 792 ways
B)
The possible number of committes consist of 2 Democrats, 2 Republicans, and 1 Independent



= 180 ways
C)
From above,
The possible number of committes chosen ( chosen 5 people from a collection of 12 people)= 792 ways
The possible number of committes consist of 2 Democrats, 2 Republicans, and 1 Independent = 180 ways
Now,
the probability that the committee consists of 2 Democrats, 2 Republicans, and 1 Independent = 180 / 792 = 0.2273
D)
Possible Committee:
i) 4 Democrats, 1 Republicans
ii) 4 Democrats, 1 Independent
iii) 5 Democrats
Now,
The possible number of committees that consist of at least 4 Democrats



= 96 ways
Related Solutions
A team of size m has to be chosen from a group of n people (m...
A committee of 4 is chosen at random from a group of 7 women 5 men....
Suppose that a committee of 12 people is selected in a random manner from a group...
Find the probability that a randomly chosen group of 9 people have no birthdays in common,...
A committee of 2 women and 6 men is to be chosen randomly from a group...
5 people from group are given an ID ranging from 1-9 independent from each other's ID....
John measured the total playing time of 35 randomly chosen CDs from his very large collection...
In a group of 12 astronauts, 5 of them are experts in exobiology. Out of the...
In a group of 12 astronauts, 5 of them are experts in exobiology. Out of the...
Determine the probability that in a group of 5 people, at least two share the same...
- The score recorded for student 12 for event 5 is incorrect. The score should be a...
- Formulate the outline of a precision pricing policy for a four-star hotel designed to accommodate business...
- The chosen Company is Amazon. Financial statements for the years 2016, 2017 and 2018. A. Analyze...
- With the establishment of the World Trade Organization (WTO) in 1995 (previously General Agreement on Tariffs...
- The London Private Hospital has 3 patient services departments – Adult Medicine, Obstetrics and Paediatrics. It...
- Suppose that an initially empty queue performs the following operations. enqueue(7), enqueue(3), dequeue(), front(), enqueue(8), enqueue(5),...
- Write a program that manages a list of patients for a medical office. Patients should be...
 orchestra answered 3 years ago
orchestra answered 3 years ago