Question
In: Statistics and Probability
Does a continuous random variable X exist with E(X − a) = 0, where a is...
Does a continuous random variable X exist with E(X − a) = 0,
where a is the
day of your birthdate? If yes, give an example for its probability
density function.
If no, give an explanation.
(b) Does a continuous random variable Y exist with E
(Y − b)
2
= 0, where b is
the month of your birthdate? If yes, give an example for its
probability density
function. If no, give an explanation.
Solutions
Expert Solution
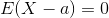
a is a day of a birthday. Or, in other words, any number belonging to R+.
This can exist.
An example to site this is:

It is known that, in such a case,


- This event cannot happen.
This is because,
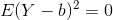
a is a month of a birthday. Or, in other words, any number belonging to R+.
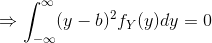
Now,
Also,
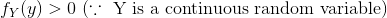
Then, integral over such a non-negetive random variable can never be 0, unless,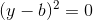
Again, this will happen, only if,
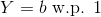
However, for a continuos random variable, there does not exist any positive probability to any fixed point.
Hence, the condition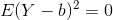 cannot be true for any continuos random
variable.
cannot be true for any continuos random
variable.
I hope this clarifies your doubt. If you're satisfied with the solution, hit the Like button. For further clarification, comment below. Thank You. :)
Related Solutions
If X is a random variable with CDF F(x) = e-e(µ-x)/β, where β > 0 and...
If X is a random variable with CDF F(x) = e-e(µ-x)/β,
where β > 0 and -∞ < µ, x < ∞; calculate the median of X.
Also, obtain the PDF of X.
Let X be a continuous random variable such that E[Xm] exists where m is some positive...
Let X be a continuous random variable such that E[Xm]
exists where m is some positive integer. Prove that if k is a
positive integer and k < m, then E[Xk] exists.
Let X be a random variable with CDF F(x) = e-e(µ-x)/β, where β > 0 and...
Let X be a random variable with CDF F(x) =
e-e(µ-x)/β, where β > 0 and -∞ < µ, x < ∞.
1. What is the median of X?
2. Obtain the PDF of X. Use R to plot, in the range
-10<x<30, the pdf for µ = 2, β = 5.
3. Draw a random sample of size 1000 from f(x) for µ = 2, β = 5
and draw a histogram of the values in the random sample...
Suppose that random variable X 0 = (X1, X2) is such that E[X 0 ] =...
Suppose that random variable X 0 = (X1, X2) is such that E[X 0 ]
= (µ1, µ2) and var[X] = σ11 σ12 σ12 σ22 . (a matrix)
(i) Let Y = a + bX1 + cX2. Obtain an expression for the mean and
variance of Y .
(ii) Let Y = a + BX where
a' = (a1, a2) B = b11 b12 0 b22 (a matrix).
Obtain an expression for the mean and variance of Y .
(ii)...
The random variable X has a continuous distribution with density f, where f(x) ={x/2−5i f10≤x≤12 ,0...
The random variable X has a continuous distribution with density
f, where f(x) ={x/2−5i f10≤x≤12 ,0 otherwise.
(a) Determine the cumulative distribution function of X.(1p)
(b) Calculate the mean of X.(1p)
(c) Calculate the mode of X(point where density attains its
maximum)
(d) Calculate the median of X, i.e. a number m such that P(X≤m)
= 1/2
(e) Calculate the mean of the random variable Y= 12−X
(f) Calculate P(X^2<121)
(15 pts) Suppose that the continuous random variable X has pdf ?(?) = { ?; 0...
(15 pts) Suppose that the continuous random variable X has
pdf
?(?) = {
?; 0 < ? < 2 2?; 5 < ? < 10 0; otherwise
a) Determine the value of c that makes this a legitimate pdf.
b) Sketch a graph of this pdf.
c) Determine the cumulative distribution function (cdf) of X.
d) Sketch a graph of this cdf.
e) Calculate ? = ?(?) and ? = ??(?).
f) What is ?(? = ?)?
g) Compute...
Let X be a continuous random variable with pdf: f(x) = ax^2 − 2ax, 0 ≤...
Let X be a continuous random variable with pdf: f(x) = ax^2 −
2ax, 0 ≤ x ≤ 2
(a) What should a be in order for this to be a legitimate
p.d.f?
(b) What is the distribution function (c.d.f.) for X?
(c) What is Pr(0 ≤ X < 1)? Pr(X > 0.5)? Pr(X > 3)?
(d) What is the 90th percentile value of this distribution?
(Note: If you do this problem correctly, you will end up with a
cubic...
2. Let X be a continuous random variable with PDF ?fx(x)= cx(1 − x), 0 <...
2. Let X be a continuous random variable with PDF ?fx(x)= cx(1 −
x), 0 < x < 1,
0 elsewhere.
(a) Find the value of c such that fX(x) is indeed a PDF.
(b) Find P(−0.5 < X < 0.3).
(c) Find the median of X.
Considering X a continuous random variable defined by the distribution function f(x) = 0 if x<1...
Considering X a continuous random variable defined by the
distribution function
f(x) = 0 if x<1
-k +k/x if 1<= x < 2
1 if 2<x
Find k.
Let X be a continuous random variable that has a uniform distribution between 0 and 2...
Let X be a continuous random variable that has a uniform
distribution between 0 and 2 and let the cumulative distribution
function F(x) = 0.5x if x is between 0 and 2 and let F(x) = 0 if x
is not between 0 and 2. Compute
1. the probability that X is between 1.4 and 1.8
2. the probability that X is less than 1.2
3. the probability that X is more than 0.8
4. the expected value of X...
ADVERTISEMENT
ADVERTISEMENT
Latest Questions
- I am new to python, and i used python 3. i have to make a new...
- The December 31, 20X8, balance sheets for Pint Corporation and its 70 percent-owned subsidiary Saloon Company...
- plot this data into a bar graph: PYTHON data=pandas.read_csv(r'data/tv_shows.txt', low_memory=False) print((data)) print((data.columns)) TV Shows : Rating...
- At 25 degrees celsius only .0640 mol of the generic salt AB2 is soluble in 1.00...
- cite 3 most important healthcare financing concern in the united states today and how expenses and...
- S Company reported the following account balances on its After Closing Trial Balance
- A.) A 700- kg car collides with a 1300- kg car that was initially at rest...
ADVERTISEMENT



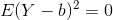
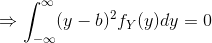

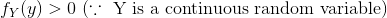
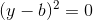
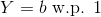
 orchestra answered 3 years ago
orchestra answered 3 years ago