Question
In: Statistics and Probability
Consider a simple linear model: yi = β1 + β2xi + εi, where εi ∼ N...
Consider a simple linear model:
yi = β1 + β2xi + εi, where εi ∼ N (0, σ2)
Derive the maximum likelihood estimators for β1 and β2. Are these the same as the estimators obtained from ordinary least squares? Is there a reason to prefer ordinary least squares or maximum likelihood in this case?
Solutions
Related Solutions
Consider a simple linear model Yi = β1 + β2Xi + ui . Suppose that we...
Consider a simple linear model Yi = β1 + β2Xi + ui . Suppose
that we have a sample with 50 observations and run OLS regression
to get the estimates for β1 and β2. We get βˆ 2 = 3.5, P N i=1 (Xi
− X¯) 2 = 175, T SS = 560 (total sum of squares), and RSS = 340
(residual sum of squares).
1. [2 points] What is the standard error of βˆ 2?
2. [4 points] Test...
Consider a simple linear regression model with nonstochastic regressor: Yi = β1 + β2Xi + ui...
Consider a simple linear regression model with nonstochastic
regressor: Yi = β1 + β2Xi + ui . 1. [3 points] What are the
assumptions of this model so that the OLS estimators are BLUE (best
linear unbiased estimates)? 2. [4 points] Let βˆ 1 and βˆ 2 be the
OLS estimators of β1 and β2. Derive βˆ 1 and βˆ 2. 3. [2 points]
Show that βˆ 2 is an unbiased estimator of β2.
Consider 2 models: yi = β1 + β2xi + ei (1) Y = X0β + e;...
Consider 2 models:
yi = β1 + β2xi + ei
(1)
Y = X0β + e;
(2)
where Equation (1) represents a system of n scalar equations for
individuals i = 1; ...; n , and
Equation (2) is a matrix representation of the same system. The
vector Y is n x 1. The matrix X0
is n x 2 with the first column made up entirely of ones and the
second column is x1; x2; ...; xn.
a. Set...
QUESTION TWO Consider the model: Yi=β1+
QUESTION TWO
Consider the
model:
Yi=β1+β2X1+Ui
Explain all the terms included in the model above
Given the model above, state the way econometricians proceed in
their analysis of an economic
problem?
Explain the importance of Ui in this
model?What are the four reasons for the inclusion of this error
term in the regression model?
What is the difference between the disturbance term and the
residual term?
Explain the meaning of statistical inference?
State the ten assumptions of the classical linear...
1. To see if the variable Xi2 belongs in the model Yi=β1+β2Xi+ui, Ramsey’s RESET test would...
1. To see if the variable Xi2 belongs
in the model
Yi=β1+β2Xi+ui,
Ramsey’s RESET test would estimate the linear model, obtaining the
estimated Yi values from this model [i.e.,
Yi=β1+β2Xi
] and then estimating the model
Yi=β1+β2Xi+α3Yi2+ui
and testing the significance of α3. Prove that, if
α3 turns out to be statistically significant in
the preceding (RESET) equation, it is the same thing as estimating
the following model directly:
Yi=β1+β2Xi+β3Xi2+ui
1. Consider the linear regression model for a random sample of size n: yi = β0...
1. Consider the linear regression model for a random sample of
size n: yi = β0 + vi ;
i = 1, . . . , n, where v is a random error
term. Notice that this model is equivalent to the one seen in the
classroom, but without the slope β1.
(a) State the minimization problem that leads to the estimation
of β0.
(b) Construct the first-order condition to compute a minimum
from the above objective function and use...
In a simple linear regression model yi = β0 + β1xi + εi with the usual...
In a simple linear regression model yi =
β0 + β1xi + εi with the
usual assumptions show algebraically that the least squares
estimator β̂0 = b0 of the intercept has mean
β0 and variance σ2[(1/n) + x̄2 /
Sxx].
Formula that you might use: For a simple linear regression model yi= α + βxi+ui, i=1,2,...,N....
Formula that you might use:
For a simple linear regression model
yi= α + βxi+ui, i=1,2,...,N.
Homework Assignment 1
1. Suppose researchers want to know the effect of elementary
school class size on students’ math scores(total score is 100),
intuitively they think there exists a negative linear relationship
between class size and students’ math scores. The researchers want
to know the marginal effect of class size on student’s math
scores.
1) Based on the background information, design an linear
regression...
Consider the model: yi = βxi + ei, i = 1,...,n where E(ei) = 0 and...
Consider the model:
yi = βxi + ei, i = 1,...,n
where E(ei) = 0 and Variance(ei) = σ2 and ei(s) are
non-correlated errors.
a) Obtain the minimum-square estimator for β and propose an
unbiased estimator for σ2.
b) Specify the approximate distribution of the β estimator.
c) Specify an approximate confidence interval for the parameter
β with confidence
coefficient γ, 0 < γ < 1.
Consider the simple linear regression: Yi = β0 + β1Xi + ui whereYi and Xi...
Consider the simple linear regression: Yi = β0 + β1Xi + ui where
Yi and Xi are random variables, β0 and β1 are population intercept
and slope parameters, respectively, ui is the error term. Suppose
the estimated regression equation is given by: Yˆ i = βˆ 0 + βˆ 1Xi
where βˆ 0 and βˆ 1 are OLS estimates for β0 and β1. Define
residuals ˆui as: uˆi = Yi − Yˆ i Show that: (a) (2 pts.) Pn i=1...
ADVERTISEMENT
ADVERTISEMENT
Latest Questions
- The main participants/ competitors in food/groceries industry?
- Company A offers you an initial salary of $150,000 with annual raises of 10% for the...
- Consider a binary classification problem where each example (observation) x has n features and class label...
- If a centrral bank were required to target inflation at zero, then when there was a...
- As a technician in a large pharmaceutical research firm, you need to produce 400. mL of...
- Better Fitness Gear applies overhead on the basis of direct labor hours. Five direct labor hours...
- 1. Superior Bake Shop sells a variety of baked goods online. Attributes of Baked Good include...
ADVERTISEMENT


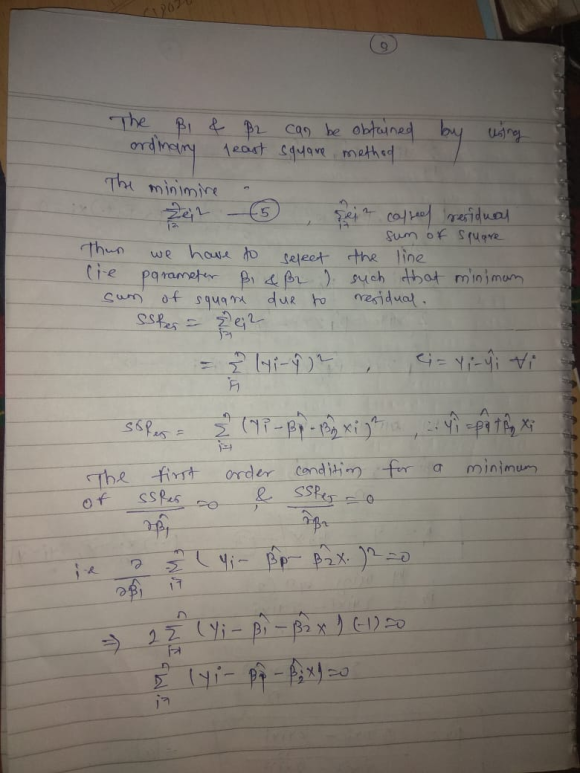


 orchestra answered 2 years ago
orchestra answered 2 years ago