Question

Consider a stick of unit length, broken into 3 pieces using the following methods: 1. We chose randomly and independently two points on the stick using a uniform PDF, and we break stick at these 2 points 2. We break the stick at a random point chosen by using a uniform PDF, and then we break the piece that contains the right end of the stick, at a random point chosen by using a uniform PDF 3. We break the stick at a random point chosen by using a uniform PDF, and then we break the larger of the 2 pieces at a random point chosen by using a uniform PDF. For each of the methods what is the probability that the three pieces we are left with can form a triangle?

Answer 1

Let there be an equilateral triangle ABC with a point P inside (or on a side) of an equilateral ΔABC drop perpendiculars PPa, PPb, PPc to its sides. By Viviani's theorem, the sum

PPa + PPb+ PPc

is independent of P and is equal to any of the triangle's altitudes. Let's take a triangle whose altitude exactly measures the length of the stick. Connect the midpoints of the sides to split ΔABC into four equal triangles, with the medial triangle in the middle. Then it is easy to surmise that the three pieces PPa, PPb, PPc form a triangle if and only if P lies inside the medial triangle. (Otherwise, one of the segments will be longer than half of an altitude, therefore making the sum of the other two shorter than half of an altitude. Thus it is clear that if P does not belong to the medial triangle one of the three triangle inequalities for PPa, PPb, PPc will fail. And the argument is reversible.)

Note also, that point P is uniquely determined by the lengths of the three segments PP_{a},PP_{b},PP_{c}.$ Indeed, the latter may be looked at as the tri linear coordinates of point P.

With this preliminaries, we may now tackle various formulations of our problem.

1. We chose randomly and independently two points on the stick using a uniform PDF, and we break stick at these 2 points

   There is 1 in 4 chance that point P falls inside the medial triangle. Point P is uniquely and randomly determined by the two break points. If the points are distributed uniformly and chosen independently, the probability that a triangle can be put together from the three pieces is 1/4.

2. We break the stick at a random point chosen by using a uniform PDF, and then we break the piece that contains the right end of the stick, at a random point chosen by using a uniform PDF

   If each of the pieces is selected with the probability 1/2, then the total probability of interest is

   1/2⋅0+1/2⋅(2⋅ln(2)−1).

   But what if the probability of selecting one of the two pieces obtained after breaking the stick grows with the length of the piece?

3. We break the stick at a random point chosen by using a uniform PDF, and then we break the larger of the 2 pieces at a random point chosen by using a uniform PDF

   Assume that the shorter piece is represented by the vertical perpendicular to PPc. Then, as above, P must lie below the vertical edge of the medial triangle. Which means that in this case, in order that the three pieces could form a triangle, P should lie inside of one (still the medial) of the three triangles. This has 1 chance in three with the probability of 1/3.

   Below, I offer a treatment of the problem based on a triangular diagram.

   

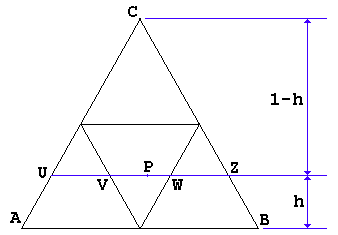
   Assume that after the first break the pieces have lengths h and (1−h), with h<(1−h), i.e. h<1/2, as expected. With h fixed, we randomlly (and uniformly) break the piece of length (1−h). The probability that the three pieces thus obtained will form a triangle clearly depends on h. It is small if h is small, and it is nearing 1 for h close to 1/2. More accurately, this probability is equal to the ratio VW/UZ, but:

   (*)	VW / UZ = h/(1-h)!

   The total probability is given as the integral of the expression in (*) from 0 to 1/2, i.e., over the range of eligible h:

   π/2 ∫0 hdh1−h=−12−ln12=ln2−12.

   The probability we are looking for is the conditional probability obtained under the assumption that h<1/2. Thus the integral must be divided by 1/2. The result, 2⋅ln(2)−1, is approximately equal to 0.386, is slightly more than 1/3, and has been verified experimentally.