Question

Two accounting professors decided to compare the variance of their grading procedures. To accomplish this, they each graded the same 10 exams, with the following results: Mean Grade Standard Deviation Professor 1 79.3 22.4 Professor 2 82.1 12.0 At the 2% level of significance, what is the decision? Multiple Choice : A. Reject the null hypothesis and conclude the variances are different. B. Fail to reject the null hypothesis and conclude the variances are different. C.Reject the null hypothesis and conclude the variances are the same. D.Fail to reject the null hypothesis and conclude the variances are the same.

Answer 1

Solution:

n₁ = 10 , n₂ = 10

= 179.3 , = 82.1

s₁ = 22.4 , s₂ = 12.0

The null and alternative hypothesis are

H₀ : ₁² =  ₂²​​  

H_a :  ₁²  ₂²​​  

Two tailed test.

d.f.₁ = n₁ - 1 = 10 - 1 = 9

d.f.₂ = n₂ - 1 = 10 - 1 = 9

= 2% = 0.02

/2 = 0.01

1 -(/2) = 0.99

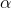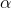The critical values are F_{1-(/2) , df1,df2} and F_{/2 , df1,df2}  

F_{1-(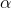/2) , df1,df2} = 0.187

F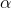_{/2 , df1,df2} = 5.351

Rejection region is F < 0.187 and F >5.351

The test statistic is

F = s₁²/s₂² = 22.4²/ 12.0²= 3.484

Test statistic 3.484 do not fall in the rejection region.

Therefore ,

D.Fail to reject the null hypothesis and conclude the variances are the same.