Question

To test the Ho: u = 40 versus Hi: u < 40, a random sample of size n = 26 is obtained from a population that is known to be normally distributed.  Complete (a) through (d).

if x = 36.8 and s = 13.9, compute the test statistic.

to = ??? (round to three decimals as needed)

a) ta = ???  (round to three decimal places.  Use a comma to separate answers)

b)  If the researcher decides to test this hypothesis at the a = 0.1 level of significance, determine the critical value(s).  Although technology or a t-distribution table can be sued to find critical value, in this problem use the t-distribution table given.

c) Draw a t-distribution that depicts the critical region.  

d) Will the researcher reject the null hypothesis?

Yes because the test statistic falls in the critical region

Yes because the test statistic does not fall in the critical region

No because the test statistic does not fall in the critical region

 

Answer 1

a) From the given information,

\begin{tabular}{|c|c|c|}

\hline \(\bar{x}\) & \(s\) & \(n\) \\

\hline 36.8 & 13.9 & 26 \\

\hline

\end{tabular}

Null hypothesis, \(H_{0}: \mu=40\)

Alternative hypothesis, \(H_{0}: \mu<40\) Calculate the test statistic value

\(t=\frac{\bar{x}-\mu}{s / \sqrt{n}}\)

\(=\frac{36.8-40}{13.9 / \sqrt{26}}\)

\(=1.174\)

Part a The test statistic value is \(1.174 .\)

The test statistic value of the one-sample hypothesis test is 1.174

b)

Level of significance, \(\alpha=0.10\) Calculate the degrees of freedom.

$$ \begin{aligned} d f &=n-1 \\ &=26-1 \\ &=25 \end{aligned} $$

Calculate the \(t-\) critical value.

$$ \begin{aligned} t-\text { critical } &=(=\mathrm{TINV}(0.1,25)) \\ &=-1.316 \quad \text { (Left tail) } \end{aligned} $$

Part \(b\) The critical value is -1.316

The \(t-\) critical value at the 0.10 level of significance with 25 degrees of the freedom is -1.316 (left tailed test).

c)

Construct the critical region graph.

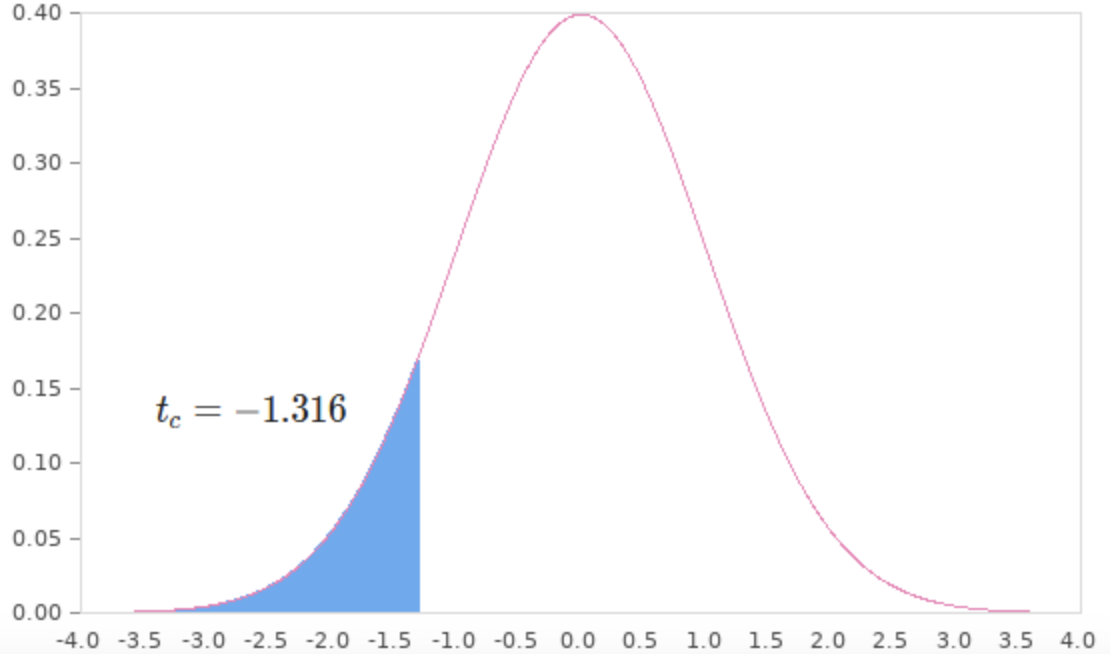
The critical region is less than -1.316

The \(t-\) critical value at the 0.10 level of significance with 25 degrees of the freedom is -1.316 (left tailed test).

d) The correct option is D No because the test statistic does not fall in the critical region.

Part d No because the test statistic does not fall in the critical region.

The test statistic value falls in the critical region, so we reject the null hypothesis and conclude that the alternative

hypothesis is true. That is \(H_{1}: \mu<40\) is true.

Part a

The test statistic value is 1.174.

Part b

The critical value is -1.316

Part c

The critical region is less than -1.316

Part d

No, because the test statistic does not fall in the critical region.