Question
In: Math
Use the mid-point rule with n = 2 to approximate the area of the region bounded...
Use the mid-point rule with n = 2 to approximate the area of the region bounded by y equals the cube root of the quantity 16 minus x cubed y = x, and x = 0.
Solutions
Expert Solution
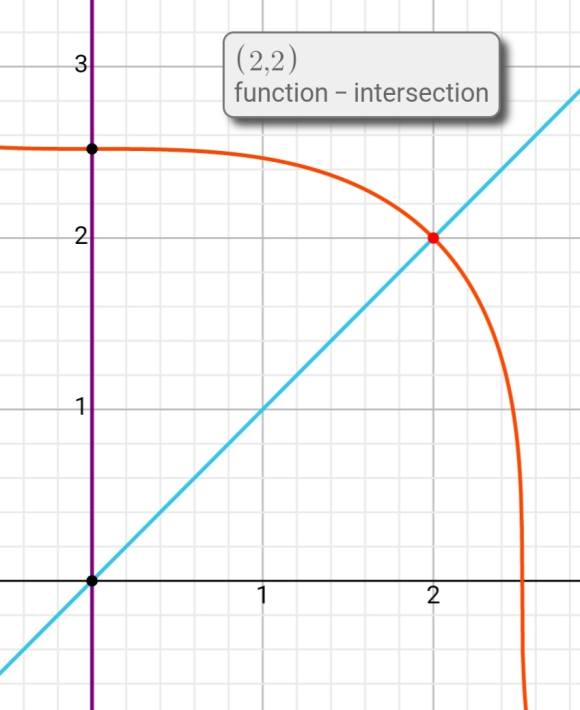
Hello Dear, I am not able to find the function written in words! Please check below if I have found correct functions
y=(16-x^3)^(1/3), y=x, and x=0
if I am wrong, please tell me the function in coments, I will
upload solution for that! 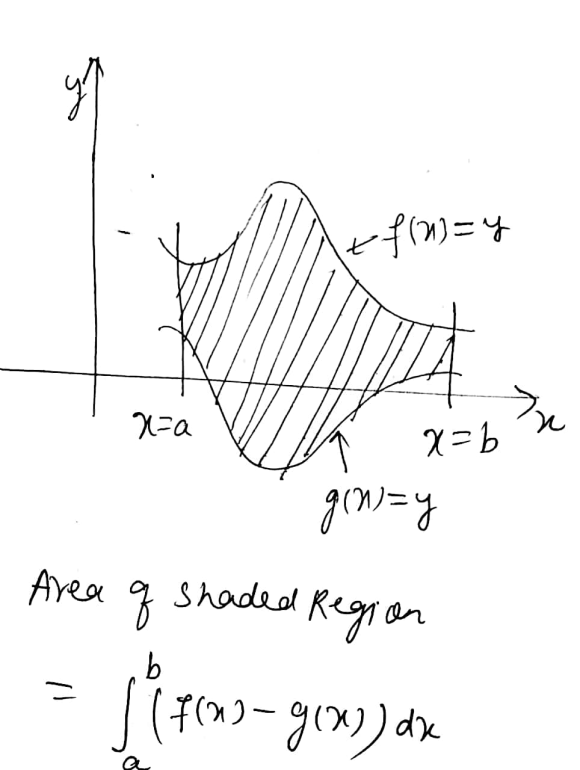


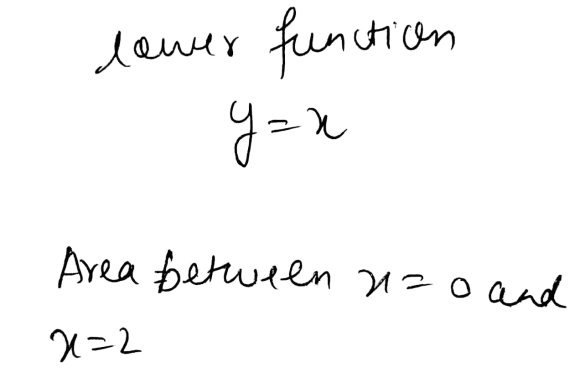
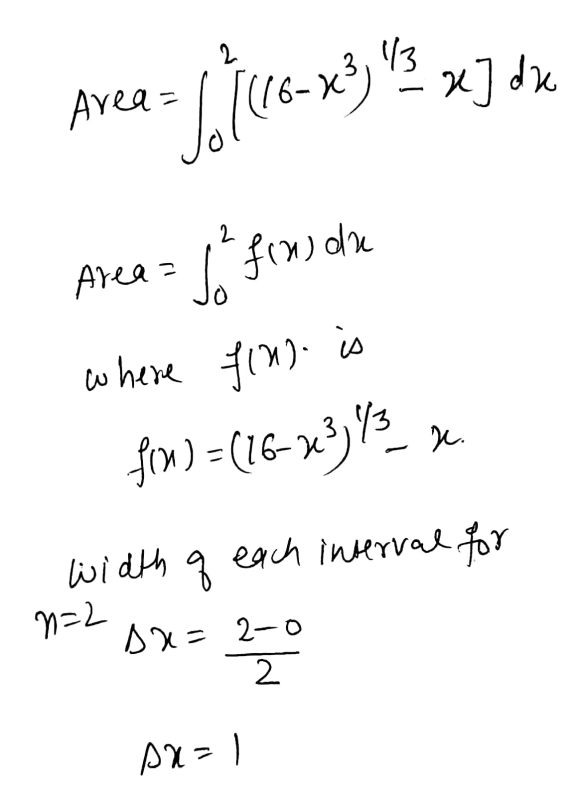



Related Solutions
Use Simpson's Rule with n = 10 to approximate the area of the surface obtained by...
Use Simpson's Rule with n = 10 to approximate the area of the
surface obtained by rotating the curve about the x-axis. Compare
your answer with the value of the integral produced by your
calculator. (Round your answer to six decimal places.)
y = e^−x^2, 0 ≤ x ≤ 5
Use Simpson's Rule with n = 10 to approximate the area of the surface obtained by...
Use Simpson's Rule with n = 10 to approximate the area
of the surface obtained by rotating the curve about the
x-axis. Compare your answer with the value of the integral
produced by your calculator. (Round your answer to six decimal
places.)
y = x + sqrt x, 2 ≤ x ≤ 5
Use Simpson's Rule with n = 10 to approximate the area of the surface obtained by...
Use Simpson's Rule with n = 10 to approximate the area
of the surface obtained by rotating the curve about the
x-axis. Compare your answer with the value of the integral
produced by your calculator. (Round your answer to six decimal
places.)
y = x + sqrt x, 2 ≤ x ≤ 5
Sketch and find the area of the region bounded by the curves ?=?+? and ?=?2−?.
Sketch and find the area of the region bounded by the curves
?=?+? and ?=?2−?.
Find the area of the region bounded by the parabolas x = y^2 - 4 and...
Find the area of the region bounded by the parabolas x = y^2 - 4
and x = 2 - y^2
the answer is 8 sqrt(3)
a) Find the area of the region bounded by the line y = x and the...
a) Find the area of the region bounded by the line y = x and the
curve y = 2 - x^2. Include a sketch.
Find the volume of the solid created when rotating the region in
part a) about the line x = 1, in two ways.
Use Simpson’s Rule with n = 4 to approximate the value of the definite integral ∫4...
Use Simpson’s Rule with n = 4 to approximate the value of the
definite integral ∫4 0 e^(−x^2) dx. (upper is 4, lower is 0)
Compute the following integrals (you may need to use Integration
by Substitution):
(a) ∫ 1 −1 (2xe^x^2) dx (upper is 1, lower is -1)
(b) ∫ (((x^2) − 1)((x^3) − 3x)^4)dx
find the area of the region bounded by the curves √ x + √y = 1...
find the area of the region bounded by the curves √ x + √y = 1
and the coordinate axis.
What is the area of the region bounded by given curves, x^2 + 4x - 2y + 2 = 0 and y = 0?
What is the area of the region bounded by given curves, x^2 + 4x - 2y + 2 = 0 and y = 0?
Use the Trapezoidal Rule, the Midpoint Rule, and Simpson's Rule to approximate the given integral with...
Use the Trapezoidal Rule, the Midpoint Rule, and Simpson's Rule
to approximate the given integral with the specified value of n.
(Round your answers to six decimal places.)
2
1
6 ln(x)
1 + x
dx, n = 10
ADVERTISEMENT
ADVERTISEMENT
Latest Questions
- Write at least one paragraph with a minimum of 100 words on the Tang Dynasty period...
- C++ How can I print out the subtrees in my self-balancing tree? What I would like...
- Describe how the Rational User Process can accommodate agile process. Specify in what phases and what...
- You are the lead auditor performing a walkthrough of the bank reconciliation performed by the company...
- 5. In recent years, about twenty states have passed so-called medical marijuana laws. Typically, these laws...
- What roles does HRM perform relative to each international business strategy of ethnocentric, geocentric and polycentric...
- Explain why the client congestion window(cwnd) size varies differently for different load conditions. In context to...
ADVERTISEMENT
 milcah answered 3 years ago
milcah answered 3 years ago