Question

There are two reasonable approximations to consider for the pencil in this problem: a cylinder and a thin rod. However, in this problem, we will treat the pencil as a uniform thin rod of length 15.0 cm and mass 10.0 g.

The pencil rotates about an axis perpendicular to the plane of the figure. Which of the labeled points is the point that the axis of rotation passes through?

Answer 1

Concepts and reason

The concepts used to solve this problem are weight, center of mass, free body diagram, frictional force, and torque. First, use the concept of center of mass, weight, normal force, and friction force to draw the free body diagram of the pencil and show all forces that act on it.. Next, use the concept of the torque, and determine the point through which the axis of rotation for the pencil passes.

Fundamentals

Free body diagram (FBD): A free body diagram is a graphical representation of the applied forces and their resultant effect (also referred as reaction) on a body in a given condition. Normal force: It is defined as a contact force which is applied to the body against the net force on the body. The direction of the normal force is normal to the surface. Frictional force: The frictional force is a type of contact force which opposes the relative motion of the body. It is directly proportional to the normal reaction force. It always acts in the direction, opposite to the direction of motion. Torque: It is the rotational force on a body about a point. It is the product of the force and the perpendicular distance of the line of action of force from the center of the rotation. since the rotational motion of a body is defied about an axis of rotation, torque is also defined about an axis of rotation. Write the expression for the weight as, \(W=m g\)

Here, \(m\) is the mass of the object and \(g\) represents the acceleration due to gravity. The force due to gravity or weight of an object, always acts in vertically downward direction. Center of mass: It is the point on the body where whole mass of the body is assumed to be concentrated and thus the net weight of the body is assumed to act at the center of mass. The center of mass of the thin rod with uniform cross section is at the mid-span, that is, at the center of the rod.

 

The free body diagram of the pencil with the forces that act on it, is drawn as,

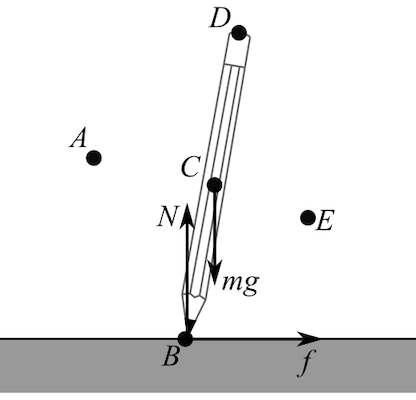
Here, \(N\) is the normal force, \(m g\) is the weight of the pencil, \(f\) is the friction force, point \(C\) is the center of mass of the pencil.

 

Draw the free body diagram of the pencil which touches the surface at point \(\mathrm{B}\). The normal force from the surface acts on the pencil at point \(\mathrm{B}\). The weight of the pencil acts in vertically downward direction at the center of mass of the pencil, which is at point \(C\). There is a friction force which oppose the motion of the pencil on the surface.

 

since the pencil touches the surface at point B, the weight of the pencil produces a torque and makes the pencil rotate about this point \(\mathrm{B}\), and this is the point through which the axis of rotation for the pencil passes.

The axis of rotation of the pencil passes through point \(B\).

 

The weight of the pencil acts in vertically downward direction at the center of mass of the pencil, that is, at point \(\mathrm{C}\). since, the pencil touches the surface at point B, the force due to weight of the pencil produces a torque and makes the pencil rotate about point \(\mathrm{B}\).

 

The axis of rotation of the pencil passes through point \(B\).