Question

A proton follows the path shown in (Figure 1). Its initial speed is v0 = 1.4 x 10^6 m/s.

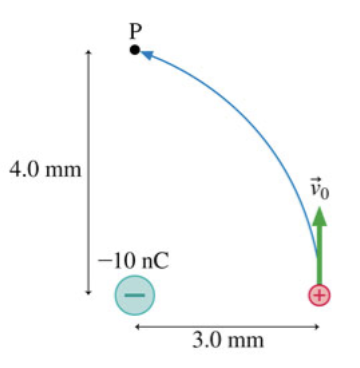
Part A What is the proton's speed as it passes through point P? Express your answer to two significant figures and include the appropriate units.

Answer 1

Initial speed of the proton, \(v_{0}=1.4 \times 10^{6} \mathrm{~m} / \mathrm{s}\)

According to law of conservation of energy

$$ \begin{aligned} \frac{1}{2} m v_{0}^{2}+\frac{k Q q}{r_{1}} =\frac{k Q q}{r_{2}}+\frac{1}{2} m v^{2} \\ \frac{1}{2} m v^{2} =\frac{1}{2} m v_{0}^{2}+\frac{k Q q}{r_{1}}-\frac{k Q q}{r_{2}} \\ =\left[\frac{1}{2} \times 1.67 \times 10^{-27} \times\left(1.4 \times 10^{6}\right)^{2}\right] \\ +\left[\frac{9 \times 10^{9} \times 1.6 \times 10^{-19} \times\left(-10 \times 10^{-9}\right)}{3 \times 10^{-3}}\right] \\ -\left[\frac{9 \times 10^{9} \times 1.6 \times 10^{-19} \times\left(-10 \times 10^{-9}\right)}{4 \times 10^{-3}}\right] \\ =\left(1.64 \times 10^{-15}\right)-\left(4.8 \times 10^{-15}\right)+\left(3.6 \times 10^{-15}\right) \\ \frac{1}{2} m v^{2} =0.44 \times 10^{-15} \\ v =\sqrt{\frac{2 \times 0.44 \times 10^{-15}}{1.67 \times 10^{-27}}} \\=7.3 \times 10^{5} \mathrm{~m} / \mathrm{s} \end{aligned} $$

Hence the final speed of the proton is \({ 7 . 3 \times 1 0 ^ { 5 } \mathrm { m } / \mathrm { s } }\)