Question

Jack likes to go fishing. While waiting for the fishes to bite, he formulates the following model for the process: fishes bite according to a Poisson process with intensity 4 bites per hour. Biting fishes are caught independently, and on average only one in two times.

a) What is the probability that six fishes bite during the first two hours?

b) What is the probability that he fails to catch any fishes during the first two hours?

c) What is the probability that, during the first two hours, six fishes bite and two of these are caught?

Answer 1

a) For a 2 hour period, there would be on an average 4*2 = 8 bites. Therefore the probability that 6 fishes bite during the first two hours is computed here using the poisson probability distribution formula as:

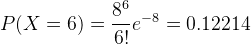
Therefore 0.12214 is the required probability here.

b) Probability that he fails to catch any fish during the two hour period. We saw that there are 8 averages bites in 2 hour period. Therefore there would be on an average 8*0.5 = 4 catches in the 2 hour period. Probability of no catch therefore is computed here as:

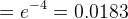
Therefore 0.0183 is the required probability here.

c) Probability that during the first 2 hours, 6 fishes bite and 2 of these are caught. We use the poisson distribution for the first part of probability and binomial distribution for the second part.

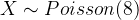
Therefore 0.0286 is the required probability here.