Question
In: Statistics and Probability
Suppose that the average trip time from your house to school on the train is 24...
Suppose that the average trip time from your house to school on the train is 24 minutes and that the standard deviation of the population is 4 minutes (sigma=4). We are interested to know whether the average trip time on Thursdays is shorter. We study a sample of 49 trips on Thursdays and the average is 22.75 minutes. Execute a hypothesis test at alpha=10% that the average trip time on Thursdays is shorter (that is, that it requires a smaller number of minutes). State Ho, Ha, calculate the appropriate statistic, p-value, state whether you reject Ho vs. not and state your conclusion in plain English.
A) What is the largest number of minutes that will allow you to reject Ho?
B) What is the probability that you will reject Ho if mu is actually 23.375 minutes?
C) Fill in the probabilities in the table below. Also indicate alpha, beta and power. D)What test concludes Ho is true in population Ho not true in population Reject Ho Not reject Ho
D) Fill in the probabilities in the table below. Also indicate alpha, beta and power.
{What test concludes; Ho is true in population ; Ho not true in population }
{Reject Ho ; ; }
{Not reject Ho ; ; }
Solutions
Expert Solution
-
Objective: To test whether the average trip time on from house to school onThursdays is shorter than the usual 24 minutes.
Let
 denote the average trip time on from Jhouse to school onThursdays.
The Null and Alternative Hypothesis can be expressed as
follows:
denote the average trip time on from Jhouse to school onThursdays.
The Null and Alternative Hypothesis can be expressed as
follows: -
H0:
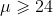 Vs
Vs 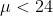 at
at
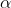 =0.10
=0.10As mentioned in the problem, since, the population standard deviation
 is known (
is known ( = 4), the appropriate test to test the above hypothesis would be a
one sample Z test for mean:
= 4), the appropriate test to test the above hypothesis would be a
one sample Z test for mean: But before running this test, we must ensure that the data satisfies the assumptions of this test:
- The study variable is continuous - The observations are collected randomly - The data is normally distributed
Assuming that all the assumptions are satisfied:
The test statistic is given by:
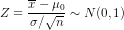
with critical value Z
 2.3164
2.3164Substituting the given values in the test statistic:
Z= (22.75-24)/(4/sqrt(49))
-
= -2.1875
To obtain the p-value of the test, p(Z< -2.1875) = 0.01435
-
Since, the p-value obtained =0.01435 < 0.1, we reject H0. We may conclude that the data does provide sufficient evidence to support the claim that the average trip time on from Jhouse to schoolonThursdays is shorter than the usual 24 minutes.
-
From the critical region of the test, the smallest number of minutes that will allow us to reject Ho would be: 2.3164
-
We have to find Xcritical such that
-
-2.3164= (Xcritical -24)/4
-
Xcritical=24-2.3164*4
-
=14.7344 minutes.
-
The probability that we would reject Ho if mu is actually 22.75 minutes is nothing but the probability of rejecting Ho, when it is fales. This is nothing but the power of the test.
- Assume that H0 is true, and
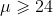
- Find the percentile value corresponding to If p(Z < zb = 0.1, then zb= -2.3164 b=24-2.3164*(4/sqrt(49)) =22.6763 minutes.
- Now, assuming that H0 is false, and instead
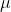 =22.75
=22.75 - Finding the power by calculating the probability of getting a value more extreme than b from Step 2 in the direction of Ha. Here, we need to find p(Z > z) where
=(b-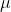 )/(4/sqrt(49)) =
(22.6763-22.75)/(4/sqrt(49))
)/(4/sqrt(49)) =
(22.6763-22.75)/(4/sqrt(49))
=-0.1289
we find that p(Z< -0.1289) = 0.4487
Beta = 1 - Power = 1 - 0.4487 = 0.5513 and Alpha, as fixed in the problem is 0.1.
Power = 0.4487, Beta=0.5513 , alpha=0.1
Related Solutions
Sketch a speed-time graph showing your trip from home to school. A. Circle and label all...
Convert the following 24-hour PA person trip matrix to OD vehicle trip matrix. Assume the average...
Suppose that we are at time zero. Passengers arrive at a train station according to a...
4. (24) The average starting salary of a random sample of 100 high school students was...
The average time a subscriber of a local newspaper The News spends reading it is 24...
Suppose that TCP's current estimated values for the round-trip time (estimatedRTT) and deviation in the RTT...
Suppose a firm has average total cost = 54 and average variable cost = 24. If...
In C, 1) Create variables for: your first and last name total round trip to school...
What is the round-trip travel time of light from Earth to Neptune (at a distance of...
A high school teacher is interested to compare the average time for students to complete a...
- Marin Construction Company began work on a $424,000 construction contract in 2020. During 2020, Marin incurred...
- What is the most important characteristic of muscle architecture that dictates its maximal force production? a.)...
- A chemist weighed out 1.654 g of a mixture containing unknown amounts of iron (Fe) and...
- Question 21 Vibrios are bacteria that have..... A. Comma shape B. Rod shape C. All are...
- When exposed to air, aluminum metal, Al, reacts with oxygen, O2, to produce a protective coating...
- Six Measures of Solvency or Profitability The following data were taken from the financial statements of...
- Write a program, which will act as a simple four-function calculator. That is, it will read...
 denote the average trip time on from Jhouse to school onThursdays.
The Null and Alternative Hypothesis can be expressed as
follows:
denote the average trip time on from Jhouse to school onThursdays.
The Null and Alternative Hypothesis can be expressed as
follows: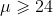 Vs
Vs 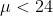 at
at
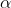 =0.10
=0.10 is known (
is known (
 2.3164
2.3164 orchestra answered 3 years ago
orchestra answered 3 years ago