Question

Each part of (Figure 1) shows one or more point charges. The charges have equal magnitudes.

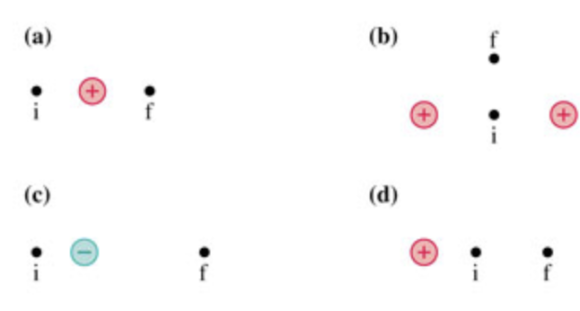
A) For case (a), if a positive charge is moved from position i to position f, does the electric potential energy increase, decrease, or stay the same?

For case (a), if a positive charge is moved from position to position, does the electric potential energy increase, decrease, or stay the same?

	Electric potential energy increases.
	Electric potential energy decreases.
	Electric potential energy stays the same.
	It's impossible to determine.

B)For case (b), if a positive charge is moved from position i to position f, does the electric potential energy increase, decrease, or stay the same?

For case (b), if a positive charge is moved from position to position, does the electric potential energy increase, decrease, or stay the same?

	Electric potential energy increases.
	Electric potential energy decreases.
	Electric potential energy stays the same.
	It's impossible to determine.

C)For case (c), if a positive charge is moved from position i to position f, does the electric potential energy increase, decrease, or stay the same?

For case (c), if a positive charge is moved from position to position, does the electric potential energy increase, decrease, or stay the same?

	Electric potential energy increases.
	Electric potential energy decreases.
	Electric potential energy stays the same.
	It's impossible to determine.

D)For case (d), if a positive charge is moved from position i to position f, does the electric potential energy increase, decrease, or stay the same? For case (d), if a positive charge is moved from position to position, does the electric potential energy increase, decrease, or stay the same?

	Electric potential energy increases.
	Electric potential energy decreases.
	Electric potential energy stays the same.
	It's impossible to determine.

Answer 1

Concepts and reason

The concept required to solve the given problem is electrostatic potential energy. Firstly, determine the relationship between the electric potential energy and the distance between the two charges using the expression of potential energy. Then, find the effect on potential energy if the distance changes. Then, determine the potential energy of the initial and final configuration in case \(\mathrm{b}\) by using the expression of potential energy and compare them. Then, determine the potential energy of the initial and final configuration in case c using the expression of potential energy and compare them. Then, determine the potential energy of the initial and final configuration in cased using the expression of potential energy and compare them.

Fundamentals

The electric potential energy of a system of two charges is as follows:

\(U=\frac{k q_{1} q_{2}}{r}\)

Here, \(r\) is the distance between the two charges \(q_{1}\) and \(q_{2}\), and \(\mathrm{k}\) is the Coulomb's constant.

 

(a) figure 1 represents the configuration of charges in case a.

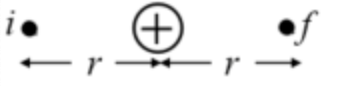
Figure 1: case a

The distance of positive charge from points i and \(\mathrm{f}\) is the same and equals r. All the charges have the same magnitude and are positive. The electric potential energy of a system of two charges is as follows:

\(U=\frac{k q_{1} q_{2}}{r}\)

The two charges are the same and are equal to q. The electric potential energy for position i is as follows:

\(U_{i}=\frac{k q^{2}}{r}\)

The electric potential energy for position \(\mathrm{f}\) is as follows:

\(U_{f}=\frac{k q^{2}}{r}\)

On comparing both equations, \(U_{i}=U_{f}\)

Thus, electric potential energy stays the same.

Part a

The electric potential energy stays the same.

The electric potential energy depends on the magnitude and sign of charges and the distance between them. The potential energy of the system of two charges when the positive charge is at position i is equal to that of the system when the positive charge is at position \(\mathrm{f}\).

 

(b) The figure 2 represents the configuration of charges in case \(\mathrm{b}\).

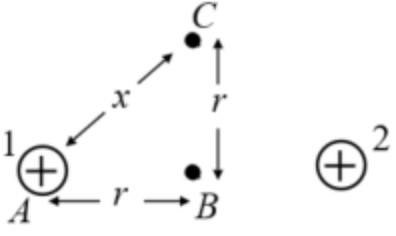
Figure 2: case \(\mathrm{b}\)

The distance between the final position \(\mathrm{f}\) and the charge 1 is \(\mathrm{x}\). Use Pythagoras theorem and find the distance between the final position and charge 1 . In triangle \(\mathrm{ABC}\), \(A C^{2}=A B^{2}+B C^{2}\)

Substitute \(x\) for \(A-C, r\) for \(A B\) and \(B C\) in the above expression.

\(x^{2}=r^{2}+r^{2}\)

\(=2 r^{2}\)

\(x=\sqrt{2} r\)

The electric potential energy is inversely proportional to the distance between the charged particles. The distance between charges at \(\mathrm{A}\) and \(\mathrm{B}\) is \(\mathrm{r}\) initially. Finally, the distance between the charges at \(\mathrm{A}\) and \(\mathrm{C}\) become \(\sqrt{2} r\) Thus, the distance between the charges increase due to which the electric potential energy of the configuration decreases. The electric potential energy is inversely proportional to the distance. Thus, when the distance increases, the potential energy does not increase or stays the same.

The distance between the initial position i from positive charge is \(\mathrm{r}\) and the distance between the final position \(\mathrm{f}\) and the positive charge is \(\sqrt{2}\) r. The charges have the same magnitude and signs such that the only term that can be compared is the distance between the charges in both positions. The distance is inversely proportional to the electric potential energy such that the electric potential energy decreases as the distance increases.

 

The electric potential energy of a system of two charges is as follows:

\(U=\frac{k q 1 q 2}{r}\)

The two charges are same and are equal to q. The electric potential energy for position i is as follows:

\(U_{i}=\frac{k q^{2}}{r}+\frac{k q^{2}}{r}+\frac{k q^{2}}{(2 r)^{2}}\)

\(=\frac{5 k q^{2}}{2 r}\)

The electric potential energy for position \(\mathrm{f}\) is as follows:

$$ U_{f}=\frac{k q^{2}}{x}+\frac{k q^{2}}{x}+\frac{k q^{2}}{2 r} $$

\(=\frac{2 k q^{2}}{x}+\frac{k q^{2}}{2 r}\)

Substitute \(\sqrt{2} r\) for \(x\) in the above expression.

\(U_{f}=\frac{2 k q^{2}}{\sqrt{2} r}+\frac{k q^{2}}{2 r}\)

\(=\left(\sqrt{2}+\frac{1}{2}\right) \frac{k q^{2}}{r}\)

On comparing both equations, \(U_{i}>U_{f}\)

Thus, electric potential energy decreases.

Part \(b\) The electric potential energy decreases.

The initial configuration's potential energy is calculated between the charges 1 and 2, charges 1 and charge at B, and charges at \(B\) and 2. Similarly, the final configuration's potential energy is calculated between the charges 1 and 2, charges 1 and charge at \(C\), and charges at \(C\) and 2.

 

(c) figure 3 represents the configuration of charges in case \(\mathrm{c}\).

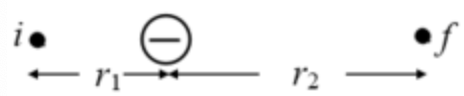
Figure 3: case \(\mathrm{c}\)

The distance of positive charge from points i and \(f\) are different. The charge at i is positive, and the middle charge is negative but has the same magnitude as that of charge at i. The electric potential energy of a system of two charges is as follows:

\(U=\frac{k q_{1} q_{2}}{r}\)

The electric potential energy depends on the magnitude and sign of charges and the distance between them. The middle charge is negative, due to which the initial potential energy is negative. The distance between the charges increases \(\left(r_{2}>r_{1}\right)\) due to which the magnitude of the electric potential energy of the configuration decreases. The magnitude decreases, but the potential energy has a negative charge such that the value of energy decreases. Thus, potential energy does not decrease or stays the same.

The distance between the initial position I from the positive charge is \(\mathrm{r} 1\) and the distance between the final position \(\mathrm{f}\) and the positive charge is r2. The charges have the same magnitude but different signs such that the potential energy has a negative value. The distance between the charges increases such that the magnitude of potential energy decreases since the sign is negative; the potential energy increases.

 

The electric potential energy of a system of two charges is as follows:

\(U=\frac{k q_{1} q_{2}}{r}\)

The electric potential energy for position i is as follows:

\(U_{i}=\frac{k q_{1} q_{2}}{r_{1}}\)

Substitute g for \(\mathrm{q} 1\) and \(-\mathrm{q}\) for \(\mathrm{q} 2\) in the above expression. \(U_{i}=-\frac{k q^{2}}{r_{1}}\)

The electric potential energy for position \(f\) is as follows:

\(U_{f}=\frac{k q_{1} q_{2}}{r_{2}}\)

Substitute g for \(q 1\) and \(-q\) for \(q 2\) in the above expression. \(U_{f}=-\frac{k q^{2}}{r_{2}}\)

On comparing both equations, \(U_{i}<U_{f}\)

Thus, electric potential energy increases.

Part c The electric potential energy increases.

In the case of negative quantities, the more is the magnitude; the less will be the value. The magnitude of the initial configuration was greater than the magnitude of the final configuration. But, the quantities are negative such that configuration 1 has less energy than configuration 2.

 

(d) figure 4 represents the configuration of charges in case \(\mathrm{d}\).

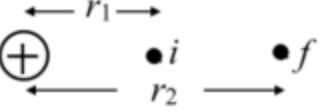
Figure 4: case d

The distance of positive charge from points i and \(f\) are different. The charge at i is positive, and the middle charge is also positive. The electric potential energy of a system of two charges is as follows:

\(U=\frac{k q_{1} q_{2}}{r}\)

The electric potential energy depends on the magnitude and sign of charges and the distance between them. The distance between the charges increases \(\left(r_{2}>r_{1}\right)\) due to which the magnitude of the electric potential energy of the configuration decreases. Thus, potential energy does not increase or stays the same.

The distance between the initial position i from the positive charge is \(\mathrm{r} 1\) and the distance between the final position \(\mathrm{f}\) and the positive charge is r2. The charges have the same magnitude. The distance between the charges increases such that the magnitude of potential energy decreases.

 

The electric potential energy of a system of two charges is as follows:

\(U=\frac{k q_{1} q_{2}}{r}\)

The electric potential energy for position i is as follows:

\(U_{i}=\frac{k q_{1} q_{2}}{r 1}\)

Substitute q for \(q 1\) and \(q\) for \(q 2\) in the above expression. \(U_{i}=\frac{k q^{2}}{r 1}\)

The electric potential energy for position \(\mathrm{f}\) is as follows:

\(U_{f}=\frac{k q_{1} q_{2}}{r 2}\)

Substitute q for \(q 1\) and \(q\) for \(q 2\) in the above expression. \(U_{f}=\frac{k q^{2}}{r_{2}}\)

On comparing both equations, \(U_{i}>U_{f}\)

Thus, the electric potential energy decreases.

Part d The electric potential energy decreases.

The charges have the same magnitude and signs such that the only term that can be compared is the distance between the charges in both positions. The distance is inversely proportional to the electric potential energy such that the electric potential energy decreases as the distance increases.

Part a

The electric potential energy stays the same.

Part b

The electric potential energy decreases.

Part c

The electric potential energy increases.

Part d

The electric potential energy decreases.