Question

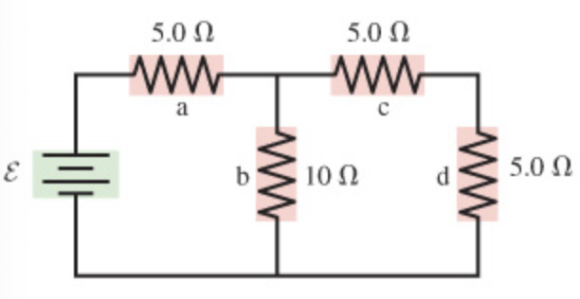
Consider the circuit shown in (Figure 1). Suppose that E = 15 V . include units with answers.

Part A: Find the current through the resistor a.

Part B: Find the potential difference across the resistor a. answer: 7.5 V

Part C: Find the current through the resistor b.

Part D: Find the potential difference across the resistor b.

Part E: Find the current through the resistor c.

Part F: Find the potential difference across the resistor c.

Part G: Find the current through the resistor d.

Part H: Find the potential difference across the resistor d.

Answer 1

Solution The resistances c and d are in series 

$$\begin{aligned} R_{x} &=R_{e}+R_{d} \\ &=5 \Omega+5 \Omega \\ &=10 \Omega \end{aligned}$$

Thus, total resistance in series is $10 \Omega$

The following diagram represents the simplified circuit diagram

Resistance $b$ and $R_{x}$ in parallel $\frac{1}{R_{p}}=\frac{1}{R_{s}}+\frac{1}{R_{s}}$

$=\frac{1}{10 \Omega}+\frac{1}{10 \Omega}$

$=\frac{1}{5}$

$R_{p}=5 \Omega$

Thus, total resistance in parallel is $5 \Omega$

 

$$\begin{array}{l} \text { The following diagram represents the simplified circuit diagram } \\ \qquad 15 \mathrm{v}=\mathrm{VM} \end{array}$$

 

Equivalent resistance in the circuit

$$\begin{aligned} R_{e q_{0}} &=R_{a}+R_{p} \\ &=5 \Omega+5 \Omega \\ &=10 \Omega \end{aligned}$$

Therefore, Equivalent resistance in the circuit is $10 \Omega$

(a) Current through the resistance a is, By Ohm's law

$\begin{aligned} I_{a} &=\frac{V}{R_{\mathrm{eq} u}} \\ &=\frac{15 \mathrm{~V}}{10} \\ &=1.5 \mathrm{~A} \end{aligned}$

Therefore, current through resistance a is $1.5 \mathrm{~A}$

(b) Potential difference through resistance a 

$\begin{aligned} V_{a} &=I_{a} R_{a} \\ &=1.5 \mathrm{~V} \times 5 \Omega \\ &=7.5 \mathrm{~V} \end{aligned}$

Therefore, potential difference across a is $7.5 \mathrm{~V}$

 

(c) Current through the resistance b By $O h m^{\prime}$ s law

$\begin{aligned} I_{b} &=R_{\text {equ }} \times \frac{I_{a}}{R_{s}+R_{x}} \\ &=10 \Omega \times \frac{1.5 \mathrm{~A}}{10 \Omega+10 \Omega} \\ &=0.75 \mathrm{~A} \end{aligned}$

Therefore, current through resistance b is $0.75 \mathrm{~A}$

 

(d)

Potential difference through resistance b

$$\begin{aligned} V_{b} &=I_{b} R_{b} \\ &=0.75 \mathrm{~A} \times 10 \Omega \\ &=7.5 \mathrm{~V} \end{aligned}$$

Therefore, potential difference across b is $\overline{7.5 \mathrm{~V}}$

(e)

Current through the resistance By $\mathrm{Ohm}^{\prime}$ s law

$I_{e}=I_{a}-I_{b}$

$$\begin{array}{l} =1.5-0.75 \\ =0.75 \mathrm{~A} \end{array}$$

Therefore, current through resistance c is $0.75 \mathrm{~A}$

(f) Potential difference through resistance $V_{e}=I_{e} R_{e}$

$$\begin{array}{l} =0.75 \mathrm{~A} \times 5 \Omega \\ =3.75 \mathrm{~V} \end{array}$$

Therefore, potential difference across c is $3.75 \mathrm{~V}$

 

(f) Potential difference through resistance $V_{e}=I_{e} R_{e}$

$$\begin{array}{l} =0.75 \mathrm{~A} \times 5 \Omega \\ =3.75 \mathrm{~V} \end{array}$$

Therefore, potential difference across c is $3.75 \mathrm{~V}$

(g) Current through the resistance d By $O h m^{\prime}$ s law

$\begin{aligned} I_{d} &=I_{a}-I_{b} \\ &=1.5-0.75 \\ &=0.75 \mathrm{~A} \end{aligned}$

Therefore, current through resistance d is $0.75 \mathrm{~A}$

 

(h) Potential difference through resistance d

$$\begin{aligned} V_{d} &=I_{d} R_{d} \\ &=0.75 \mathrm{~A} \times 5 \Omega \\ &=3.75 \mathrm{~V} \end{aligned}$$

Therefore, potential difference across d is $3.75 \mathrm{~V}$