Question

33. The College Board reports that the in 2016, the mean mathematics SAT score was 515, and the standard deviation was 116. A sample of 65 scores is chosen from the population of all SAT scores. Find the probability that the sample mean score is less than 500.

          (a) .1492      (b).8508      (c) -.13         (d) .4483     (e) .5517

36.     Refer to question 33. Would it be unusual if the sample mean were greater than 550?

          (a) No          (b) Yes

Answer 1

Solution:

Given that,

mean =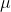  = 515

standard deviation =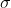  = 116

n = 65

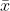= 515

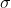
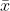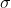=  ( /n) = (116 / 65 ) = 14.3880

33 ) P ( 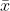  < 500 )

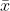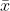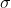
= P ( - /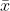) < (500 - 515 / 10.3880 )

= P ( z < - 15 / 10.3880 )

= P ( z < -1.04 )

Using z table

= 0.1492

Probability = 0.1492

36 ) P ( 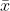  > 550 )

= 1 - P ( 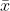  < 550 )

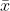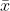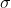
= 1 - P ( - /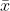) < (550 - 515 / 10.3880 )

= 1 - P ( z < 35 / 10.3880 )

= 1 - P ( z < 2.43 )

Using z table

= 1 - 0.9925

= 0.0075

Probability = 0.0075

Probability < 0.05 Sample mean is unusual Yes

Answer b) is correct.