Question

1. You are estimating costs for installing undersea cable in the Persian Gulf (aka the Arabian Gulf). You have the following information concerning installation costs:

• The material cost per kilometer for cable is $100,000.

• You are installing 100 kilometers of cable.

• The cost per kilometer for installation depends on the sea conditions (sea state). Sea State Cost/kilometer I $15,000 II $75,000

a. What would be the estimated cost of the project if you knew with certainty that, during the time you were installing the cable, you would encounter sea state I 75% of the time and sea state II 25% of the time?

b. Run a Crystal Ball calculation of the total estimated cost of the project, assuming the probability of sea state 1 is normally distributed with a mean of 25% and a standard deviation of 5%. Only sea states I and II are possible. Post your result, including your cost forecast.

c. What is your mean expected cost?

d. What estimated cost provides you 95% assurance that your actual cost will be less than that amount?

Answer 1

(a)

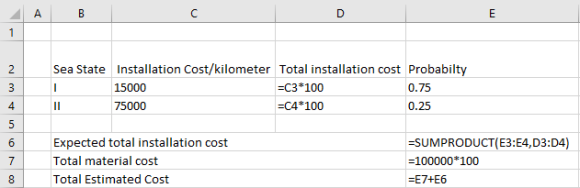
Sea State	Installation Cost/kilometer	Total installation cost	Probabilty
I	$15,000	$1,500,000	0.75
II	$75,000	$7,500,000	0.25
Expected total installation cost	$3,000,000
Total material cost	$10,000,000
Total Estimated Cost	$13,000,000

(b)

Crystal ball Report of simulation (5,000 runs)

(c)

The expected cost is $16,005,044 (the value will change slightly for each fresh simulation attempts)

(d)

Following is the 95% confidence point (right-sided)

Mean + NORMSINV(0.95)*Std. Error

= $16,005,044 + NORMSINV(0.95)*$4,222 = $16,011,989.

So, we are 95% sure that the cost will be less than $16,011,989.