Question

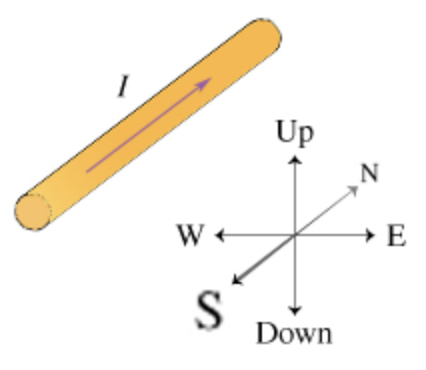
Consider a wire of length L = 0.30m that runs north-south on a horizontal surface. There is a current of I = 0.50A flowing north in the wire. (The rest of the circuit, which actually delivers this current, is not shown.) The Earth's magnetic field at this location has a magnitude of 0.50 (or, in SI units, 0.5 X10^-4 Tesla) and points north and 38 degrees down from the horizontal, toward the ground. What is the size of the magnetic force on the wire due to the Earth's magnetic field? In considering the agreement of units, recall that 1T=1N/(AxM)(Figure 1). a. Express your answer in newtons to two significant figures.

b.   Now assume that a strong, uniform magnetic field of size 0.55T pointing straight down is applied. What is the size of the magnetic force on the wire due to this applied magnetic field? Ignore the effect of the Earth's magnetic field.

The direction of the magnetic force is perpendicular to both the direction of the current flow and the direction of the magnetic field. Here is a "right-hand rule" to help you determine the direction of the magnetic force. (Figure 2)

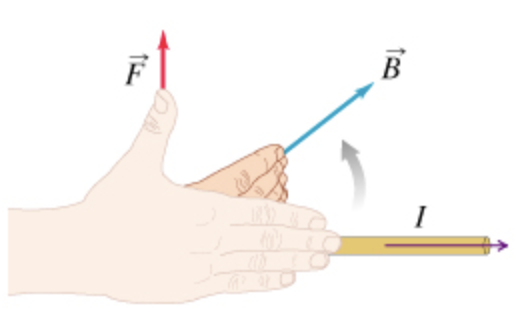
1. Straighten the fingers of your right hand and point them in the direction of the current.
2. Rotate your arm until you can bend your fingers to point in the direction of the magnetic field.
3. Your thumb now points in the direction of the magnetic force acting on

c. What is the direction of the magnetic force acting on the wire in Part B due to the applied magnetic field?

d. Assume that the applied magnetic field of size 0.55T is rotated so that it points horizontally due south. What is the size of the magnetic force on the wire due to the applied magnetic field now?

Answer 1

Concepts and reason

The concepts required to solve the problem is the Lorentz force and the right-hand rule. Initially, use the Lorentz force due to a current-carrying wire to calculate the force. Then, use the right-hand rule to determine the direction.

Fundamentals

The Lorentz magnetic force due to a current-carrying wire is, \(F=I L B \sin \theta\)

Here, \(F\) is the Lorentz force, \(I\) is the current, \(L\) is the length of the wire, \(B\) is the magnetic field, and \(\theta\) is the angle between the current and magnetic field. According to the right-hand rule, if we point our palm to the current that faces the direction of the magnetic field, the direction of thumb, which held perpendicular to both the direction of the magnetic field and the current will give the direction of the force.

 

(a) The magnetic force due to the current carrying wire is, \(F=I L B \sin \theta\)

Here, \(F\) is the Lorentz force, \(I\) is the current, \(L\) is the length of the wire, \(B\) is the magnetic field, and \(\theta\) is the angle between the current and magnetic field. Substitute \(0.50 \mathrm{~A}\) for \(I, 0.30 \mathrm{~m}\) for \(L, 0.55 \mathrm{~T}\) for \(B,\) and \(38^{\circ}\) for \(\theta .\) The force is,

$$ \begin{array}{c} F=(0.50 \mathrm{~A})(0.30 \mathrm{~m})(0.55 \mathrm{~T})\left(\sin \left(38^{\circ}\right)\right) \\ =4.6 \times 10^{-6} \mathrm{~N} \end{array} $$

The magnetic force due to the current carrying wire is \(4.6 \times 10^{-6} \mathrm{~N}\).

Part a The magnetic force due to the current-carrying wire is \(4.6 \times 10^{-6} \mathrm{~N}\).

The magnetic force due to a current-carrying wire is the product of the current flowing through the wire, length of the wire, magnetic field, and the sine of the angle between the current and magnetic field.

 

(b) The Lorentz magnetic force due to the current carrying wire is, \(F=I L B \sin \theta\)

Substitute \(0.50 \mathrm{~A}\) for \(I, 0.30 \mathrm{~m}\) for \(L, 0.55 \mathrm{~T}\) for \(B,\) and \(90^{\circ}\) for \(\theta .\) The force is,

$$ \begin{array}{c} F=(0.50 \mathrm{~A})(0.30 \mathrm{~m})(0.55 \mathrm{~T})\left(\sin \left(90^{\circ}\right)\right) \\ =8.3 \times 10^{-2} \mathrm{~N} \end{array} $$

The magnetic force due to the current carrying wire is \(8.3 \times 10^{-2} \mathrm{~N}\).

Part b The magnetic force due to the current-carrying wire is \(8.3 \times 10^{-2} \mathrm{~N}\).

The magnetic force due to a current-carrying wire is directly proportional to the current flowing through the wire and magnetic field.

 

(c) According to the right-hand role, the palm will point in the direction of the current. The palm faces to the magnetic field, the thumb kept perpendicular to the current, and the magnetic field provides the direction of force. The palm points towards the down of North, the direction of thumb is due west and the direction of force is due west.

Part c The direction of force is due west.

The direction of the force is perpendicular to the direction of current and magnetic field.

 

(d) The Lorentz magnetic force due to the current carrying wire is, \(F=I L B \sin \theta\)

Substitute \(0.50 \mathrm{~A}\) for \(I, 0.30 \mathrm{~m}\) for \(L, 0.55 \mathrm{~T}\) for \(B\) and \(90^{\circ}\) for \(\theta .\) The force is,

$$ \begin{array}{c} F=(0.50 \mathrm{~A})(0.30 \mathrm{~m})(0.55 \mathrm{~T})\left(\sin \left(0^{\circ}\right)\right) \\ =0 \mathrm{~N} \end{array} $$

The magnetic force due to the current carrying wire is \(8.3 \times 10^{-2} \mathrm{~N}\).

Part d The magnetic force due to the current carrying wire is \(8.3 \times 10^{-2} \mathrm{~N}\).

The magnetic force due to current carrying wire is zero when the current and magnetic field are parallel and in same direction to each other.