Question

Pricing Concepts -Transportation Engineering

A transportation firm is producing a transport service (with quantity Q trips) with the following cost and revenue functions:

Total Cost: TC=$36,000 + $200Q + $0.4Q^2

Total Revenue: TR=$900Q-$0.1Q^2

Set up a table or spreadsheet for trip output/supply (Q), price (P), total revenue (TR), marginal revenue (MR), total cost (TC), marginal cost (MC), average cost (AC), total profit (π), and marginal profit (Mπ). Establish a range for Q from 0 to 1,000 in increments of 100 (i.e., 0, 100, 200, ..., 1,000). Using this spreadsheet, create a graph with AC and MC as dependent variables and trip output/supply (Q) as the independent variable.

a) At what combination of price P and supply Q is profit maximized? Why?

b) At what price P and supply Q is average cost (AC) minimized? Why?

Answer 1

TR = 900Q - 0.1Q²

TC = 36,000 + 200Q + 0.4Q²

• P = TR/Q = 900 - 0.1Q
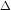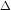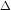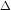• MR = TR/Q and MC = TC/Q
• AC = TC/Q = (36,000/Q) + 200 + 0.4Q
• Profit (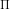) = TR - TC
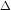
• Marginal profit = 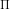/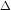Q

(1)

Data table:

Q	TR	TC	P	MR	MC	AC	Profit	Marginal profit
0	0	36,000					-36,000
100	89,000	60,000	890	890	240	600	29,000	650
200	1,76,000	92,000	880	870	320	460	84,000	550
300	2,61,000	1,32,000	870	850	400	440	1,29,000	450
400	3,44,000	1,80,000	860	830	480	450	1,64,000	350
500	4,25,000	2,36,000	850	810	560	472	1,89,000	250
600	5,04,000	3,00,000	840	790	640	500	2,04,000	150
700	5,81,000	3,72,000	830	770	720	531.43	2,09,000	50
800	6,56,000	4,52,000	820	750	800	565	2,04,000	-50
900	7,29,000	5,40,000	810	730	880	600	1,89,000	-150
1,000	8,00,000	6,36,000	800	710	960	636	1,64,000	-250

(2)

Graph:

(a) Profit is maximized (= 209,000) when Q = 700 and P = 830.

(b) AC is minimized (= 440) when Q = 300 and P = 870.