Question

Part F - Example: Finding Two Forces (Part I)

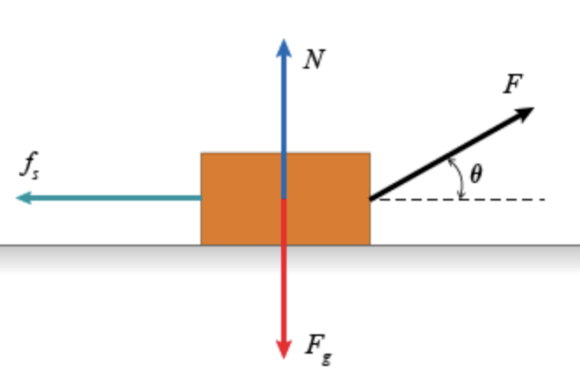
Two dimensional dynamics often involves solving for two unknown quantities in two separate equations describing the total force. The block in (Figure 1) has a mass m=10kg and is being pulled by a force F on a table with coefficient of static friction μs=0.3. Four forces act on it:

The applied force F (directed θ=30∘ above the horizontal).

The force of gravity Fg=mg (directly down, where g=9.8m/s2).

The normal force N (directly up).

The force of static friction fs (directly left, opposing any potential motion).

If we want to find the size of the force necessary to just barely overcome static friction (in which case fs=μsN), we use the condition that the sum of the forces in both directions must be 0. Using some basic trigonometry, we can write this condition out for the forces in both the horizontal and vertical directions, respectively, as:

Fcosθ−μsN=0

Fsinθ+N−mg=0

In order to find the magnitude of force F, we have to solve a system of two equations with both F and the normal force N unknown. Use the methods we have learned to find an expression for F in terms of m, g, θ, and μs (no N)

Part G - Example: Finding Two Forces (Part II)

For the situation in Part F, find the magnitude of the force F (in kg⋅m/s2) necessary to make the block move

Answer 1

Concepts and reason

The concept used to solve the problem is Newton's second law of motion. Use the horizontal and vertical equilibrium of forces to find the expression for the force that is necessary to just overcome the static friction. Use the static friction, mass, and angle of the applied force to find the magnitude of the force required to make the block move.

Fundamentals

Newton's second law of motion:

Newton's second law of motion states that "the force acting in a body is directly proportional to the mass and the acceleration of a body; and acceleration of the body is in the same direction as that of the mass of the body". The equilibrium condition for the force in horizontal and vertical components is as follows:

\(\Sigma F_{x}=0\)

\(\Sigma F_{y}=0\)

Here, the horizontal component of the force is \({F}_{x}\) and the vertical component of the force is \({F}_{y}\) The expression for Newton's second law of motion is as follows:

\(F=m a\)

Here, force is \(\mathrm{F}\), mass of the body is \(\mathrm{m}\), and acceleration of the body is a. Write the equilibrium equation for the force vectors.

$$ \sum F=0 $$

\(F_{1}+F_{2}+\ldots+F_{n}=0\)

Here, the first force acting on the subject is \(F_{1}\), second force acting on the object is \({F}_{2}\), and the nth force acting on the object is \({ }^{F_{n}}\)

 

(F) Consider a block having a mass being pulled by a force on a table.

Here, normal reaction force is \(\mathrm{N}\) and the coefficient of the static friction is \(\mu_{s}\). From the diagram, Write the expression for the horizontal equilibrium equation for the force vector.

\(F \cos \theta-f_{s}=0\)

Here, angle subtended by the force vector \(F\) is \(\theta\) and the frictional force is \(f_{s}\).

Substitute \(\mu_{s} N_{\text {for }} f_{s}\)

\(F \cos \theta-\mu_{s} N=0\)

$$ \begin{aligned} \mu_{s} N &=F \cos \theta \\ N &=\frac{F \cos \theta}{\mu_{s}} \end{aligned} $$

Write the expression for the vertical equilibrium for the force vector.

\(F \sin \theta+N-F_{g}=0\)

Substitute \(F \cos \theta / \mu_{s}\) for \(N\) and \(m g\) for \(F_{g}\)

\(F \sin \theta+\frac{F \cos \theta}{\mu_{s}}-m g=0\)

$$ \begin{aligned} F\left(\mu_{s} \sin \theta+\cos \theta\right) &=\left(\mu_{s}\right) m g \\ F &=\frac{\left(\mu_{s}\right) m g}{\mu_{s} \sin \theta+\cos \theta} \end{aligned} $$

Part F

The relation for the magnitude of force \(\mathrm{F}\) is \(\mathbf{F}=\left(\boldsymbol{\mu}_{\mathrm{s}}\right) \mathrm{mg} /\left(\boldsymbol{\mu}_{\mathrm{s}} \sin \boldsymbol{\theta}+\cos \boldsymbol{\theta}\right)\)

 

(G) From equation (1), \(F=\frac{\left(\mu_{s}\right) m g}{\mu_{s} \sin \theta+\cos \theta}\)

Substitute \(10 \mathrm{~kg}\) for \(m, 0.3\) for \(\mu_{s}, 30^{\circ}\) for \(\theta,\) and \(9.8 \mathrm{~m} / \mathrm{s}^{2}\) for \(g\) in Equation (1)

\(F=\frac{(0.3)(10 \mathrm{~kg}) 9.8 \mathrm{~m} / \mathrm{s}^{2}}{(0.3) \sin 30^{\circ}+\cos 30^{\circ}}\)

\(=\frac{3 \mathrm{~kg}\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right)}{(0.3) \sin 30^{\circ}+\cos 30^{\circ}}\)

\(=28.937 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}^{2}\)

Part G

The magnitude of force F necessary to make the block move is \(28.937 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}^{2}\).

The magnitude of the force needed to make the block move depends upon the static friction, mass, and angle of the applied force.