Question

75% of owned dogs in the United States are spayed or neutered. Round your answers to four decimal places. If 41 owned dogs are randomly selected, find the probability that

a. Exactly 29 of them are spayed or neutered. _____
b. At most 33 of them are spayed or neutered. _____  
c. At least 31 of them are spayed or neutered._____
d. Between 29 and 33 (including 29 and 33) of them are spayed or neutered. _____

Answer 1

Solution:

Given that,

P = 0.75

1 - P = 0.25

n = 41

Here, BIN ( n , P ) that is , BIN (41 , 0.75)

then,

n*p = 41*0.75 = 30.75 > 5

n(1- P) = 41*0.25 = 10.25 > 5

According to normal approximation binomial,

X Normal

Mean = 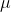= n*P = 30.75

Standard deviation = =n*p*(1-p) = 41*0.75*0.25 = 7.6875

We using countinuity correction factor

a)

P(X = a) = P( a - 0.5 < X < a + 0.5)

P(28.5 < x < 29.5) = P((28.5 - 30.75)/ 7.6875) < (x - ) /  < (29.5 - 30.75) / 7.6875) )

= P(-0.812 < z < -0.451)

= P(z < -0.451) - P(z < -0.812)

= 0.3260 - 0.2084

Probability = 0.1176

b)

P( X a ) = P(X < a + 0.5)

P(x < 33.5) = P((x - ) / < (33.5 - 30.75) / 7.6875)

= P(z < 0.992)

Probability = 0.8394

c)

P(X a ) = P(X > a - 0.5)

P(x > 30.5) = 1 - P(x < 30.5)

= 1 - P((x - ) / < (30.5 - 30.75) / 7.6875)

= 1 - P(z < -0.090)

= 1 - 0.5359

= 0.4641

Probability = 0.4641

d)

P(b X a) = P( b - 0.5 < X < a + 0.5)

P(28.5 < x < 33.5) = P((28.5 - 30.75)/ 7.6875) < (x - ) /  < (33.5 - 30.75) / 7.6875) )

= P(-0.812 < z < 0.992)

= P(z < 0.992) - P(z < -0.812)

= 0.8394 - 0.2084

Probability = 0.6310