Question

The four 1.0 g spheres shown in the figure are released simultaneously and allowed to move away from each other.

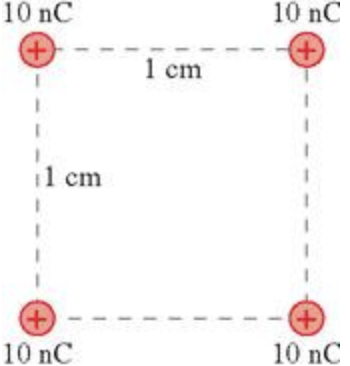
What is the speed of each sphere when they are very far apart?

Answer 1

Concepts and reason

The main concept used to solve the problem is electrostatic potential energy and kinetic energy. Initially, calculate total electrostatic potential energy of the system by calculating electrostatic potential energy between each pair. Later, when spheres are released, they start accelerating due to repulsive electrostatic force between them and this electrostatic potential energy starts getting converted into kinetic energy. Finally, When the separation between them gets sufficiently large, electrostatic energy becomes negligible as it gets totally converted into kinetic energy of the spheres.

Fundamentals

Electrostatic energy between two-point charges separated by a distance ' \(r\) ' is defined as the amount of work done in bringing together charges initially separated by infinite distance to the final separation distance \(^{\prime} r\) :

If \(Q 1\) and \(Q 2\) are two charges separated by a distance \(^{\prime} r\); then electrostatic energy U between them is:

\(U=\frac{Q_{1} Q_{2}}{4 \pi \varepsilon_{0} r}\)

Here \(\varepsilon_{0}\) is the permittivity of free space. \(\varepsilon_{0}=8.854187817 \ldots \times 10^{-12} F \cdot m^{-1}\)

The law of conservation of energy states that the energy of an isolated system remains conserved unless acted upon by some external force. Energy can neither be created, nor be destroyed, but can be transformed from one form to another. Here, in this case, it transforms from electrostatic potential energy to kinetic energy.

 

This figure shows the location of the charge.

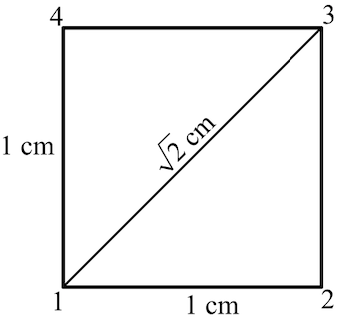
List all the charges and the distance between each pair. We have,

\(\begin{aligned} Q_{1} &=Q_{2} \\ &=Q_{3} \\ &=Q_{4} \\ &=10 \mathrm{nC} \end{aligned}\)

\(=10 \mathrm{nC}\)

Convert \(\mathrm{n} \mathrm{C}\) to coulombs.

\(Q_{1}=(10 \mathrm{nC})\left(\frac{10^{-9} \mathrm{C}}{1 \mathrm{nC}}\right)\)

\(\begin{aligned}=& 10 \times 10^{-9} \mathrm{C} \\ &=10^{-8} \mathrm{C} \end{aligned}\)

And distance is,

\(\begin{aligned} r_{12} &=r_{23} \\ &=r_{34} \\ &=r_{14} \\ &=1 \mathrm{~cm} \end{aligned}\)

Convert from centimeter to meter.

\(r_{12}=(1 \mathrm{~cm})\left(\frac{10^{-2} \mathrm{~m}}{1 \mathrm{~cm}}\right)\)

\(=10^{-2} \mathrm{~m}\)

The diagonal distance is,

\(r_{13}=r_{24}\)

\(=\sqrt{1^{2}+1^{2}}\)

\(=(\sqrt{2} \mathrm{~cm})\left(\frac{10^{-2} \mathrm{~m}}{1 \mathrm{~cm}}\right)\)

\(=1.41 \times 10^{-2} \mathrm{~m}\)

The mass of the charge is,

\(\begin{aligned} m_{1} &=m_{2} \\ &=m_{3} \\ &=m_{4} \\ &=1 \mathrm{~g} \end{aligned}\)

Convert gram to kilogram.

\(\begin{aligned} m_{1}=&(1 \mathrm{~g})\left(\frac{10^{-3} \mathrm{~kg}}{1 \mathrm{~g}}\right) \\ &=10^{-3} \mathrm{~kg} \end{aligned}\)

The pairs with same value of charges and separation distance will have same value for potential energy associated with them.

 

Calculate the potential energy of the system. \(U_{12}=\frac{Q 1 Q 2}{4 \pi \varepsilon_{0} r_{12}}\)

Here, \(Q_{1}\) and \(Q_{2}\) are charge, \(\varepsilon_{0}\) is permittivity of free space, and \(r_{12}\) is distance between charge. Substitute, \(10^{-8} \mathrm{C}\) for \(Q_{1}\) and \(Q_{2}, 8.85 \times 10^{-12} \mathrm{~F} / \mathrm{m}\) for \(\varepsilon_{0},\) and \(10^{-2} \mathrm{~m}\) for \(r_{12}\)

$$ \begin{array}{c} U_{12}=\frac{\left(10^{-8} \mathrm{C}\right)\left(10^{-8} \mathrm{C}\right)}{4 \pi\left(8.85 \times 10^{-12} \mathrm{~F} / \mathrm{m}\right)\left(10^{-2} \mathrm{~m}\right)} \mathrm{J} \\ =9 \times 10^{-5} \mathrm{~J} \end{array} $$

Similarly,

$$ U_{23}=U_{34}=U_{14}=9 \times 10^{-5} \mathrm{~J} $$

Now calculate potential energy between 1 and 3 . \(U_{13}=\frac{Q 1 Q 3}{4 \pi \varepsilon_{0} r_{13}}\)

Here, \(Q_{1}\) and \(Q_{3}\) are charge, \(r_{13}\) is distance between them. Substitute, \(10^{-8} \mathrm{C}\) for \(Q_{1}\) and \(Q_{2}, 8.85 \times 10^{-12} \mathrm{~F} / \mathrm{m}\) for \(\varepsilon_{0},\) and \(1.41 \times 10^{-2} \mathrm{~m}\) for \(r_{12}\)

$$ \begin{array}{c} U_{13}=\frac{\left(10^{-8} \mathrm{C}\right)\left(10^{-8} \mathrm{C}\right)}{4 \pi\left(8.85 \times 10^{-12} \mathrm{~F} / \mathrm{m}\right)\left(1.41 \times 10^{-2} \mathrm{~m}\right)} \\ =6.38 \times 10^{-5} \mathrm{~J} \end{array} $$

And,

$$ U_{24}=U_{13} $$

\(=6.38 \times 10^{-5} \mathrm{~J}\)

Now calculate the total energy of the system, \(U_{t o t}=U_{12}+U_{23}+U_{34}+U_{41}+U_{13}+U_{24}\)

Substitute \(9 \times 10^{-5} \mathrm{~J}\) for \(U_{12}, U_{23}, U_{34}\) and \(U_{41},\) and \(6.38 \times 10^{-5} \mathrm{~J}\) for \(U_{13}\) and \(U_{24}\)

$$ \begin{array}{c} U_{\mathrm{tot}}=\left(9 \times 10^{-5} \mathrm{~J}\right)+\left(9 \times 10^{-5} \mathrm{~J}\right)+\left(9 \times 10^{-5} \mathrm{~J}\right)+\left(9 \times 10^{-5} \mathrm{~J}\right)+\left(6.38 \times 10^{-5} \mathrm{~J}\right)+\left(6.38 \times 10^{-5} \mathrm{~J}\right) \\ =4.88 \times 10^{-4} \mathrm{~J} \end{array} $$

Electrostatic potential energy depends only upon magnitude of charges and distance between them. Hence, pairs with same value of charge and distance would have same amount of electrostatic potential energy associated with them. Electrostatic energy of each pair is added to get the total electrostatic energy of the system.

 

Consider the final velocity of each charge be \(v\). Kinetic Energy, \(K . E=\frac{1}{2} m v^{2}\)

Total Kinetic energy of system,

$$ \begin{array}{c} K . E_{t o t}=4\left(\frac{1}{2} m v^{2}\right) \\ =2 m v^{2} \end{array} $$

From the law of conservation of energy, \(K . E_{t o t}=U_{t o t}\)

Then, \(2 m v^{2}=U_{t o t}\)

Rearrange the equation \(2 m v^{2}=U_{\text {tot}}\) for \(v\). \(\boldsymbol{v}=\sqrt{\frac{U_{\mathrm{tot}}}{2 m}}\)

Substitute \(4.88 \times 10^{-4} \mathrm{~J}\) for \(U_{\mathrm{tot}}, 10^{-3} \mathrm{~kg}\) for \(m\)

\(v=\sqrt{\frac{4.88 \times 10^{-4} \mathrm{~J}}{2\left(10^{-3} \mathrm{~kg}\right)}}\)

\(=0.494 \mathrm{~m} / \mathrm{s}\)

The velocity of each sphere when they get very far apart from each other is \(0.49 \mathrm{~m} / \mathrm{s}\).

since, all 4 spheres are identical in charge, mass and position, the force experienced by any sphere due to rest 3 is same for each sphere. Hence, the acceleration or rate of change of velocity would be same for each of them.1