Question

The accuracy of a census report on a city in southern California was questioned by some government officials. A random sample of 1215 people living in the city was used to check the report, and the results are shown below.

Ethnic OriginCensus PercentSample ResultBlack10%        125        Asian3%        43        Anglo38%        471        Latino/Latina41%        510        Native American6%        56        All others2%        10        

Using a 1% level of significance, test the claim that the census distribution and the sample distribution agree.

(a) What is the level of significance?

State the null and alternate hypotheses.

H₀: The distributions are different.
H₁: The distributions are different.H₀: The distributions are the same.
H₁: The distributions are the same.    H₀: The distributions are different.
H₁: The distributions are the same.H₀: The distributions are the same.
H₁: The distributions are different.

(b) Find the value of the chi-square statistic for the sample. (Round the expected frequencies to at least three decimal places. Round the test statistic to three decimal places.)

Are all the expected frequencies greater than 5?

YesNo    

What sampling distribution will you use?

chi-squareuniform    Student's tbinomialnormal

What are the degrees of freedom?

(c) Estimate the P-value of the sample test statistic.

P-value > 0.1000.050 < P-value < 0.100    0.025 < P-value < 0.0500.010 < P-value < 0.0250.005 < P-value < 0.010P-value < 0.005

(d) Based on your answers in parts (a) to (c), will you reject or fail to reject the null hypothesis that the population fits the specified distribution of categories?

Since the P-value > α, we fail to reject the null hypothesis.Since the P-value > α, we reject the null hypothesis.    Since the P-value ≤ α, we reject the null hypothesis.Since the P-value ≤ α, we fail to reject the null hypothesis.

(e) Interpret your conclusion in the context of the application.

At the 1% level of significance, the evidence is sufficient to conclude that census distribution and the ethnic origin distribution of city residents are different.At the 1% level of significance, the evidence is insufficient to conclude that census distribution and the ethnic origin distribution of city residents are different.    

Answer 1

HYPOTHESIS TEST-

We have to perform Chi-square test for goodness of fit.

We have to test for null hypothesis

against the alternative hypothesis

Under null hypothesis, expected frequencies and few necessary calculations are as follows.

Our Chi-square test statistic is given by

Here,

Number of classes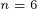

Degrees of freedom

[Using R-code '1-pchisq(14.0801,5)']

Level of significance

We reject our null hypothesis if

Here, we observe that

So, we cannot reject our null hypothesis.

Hence, based on the given data we can conclude that there is no significant evidence that the distributions are different.

ANSWER-

(a)

Level of significance

Null hypothesis is

and alternative hypothesis is

(b)

Chi-square statistic for the sample is 14.080.

Yes, all of the expected frequencies are greater than 5.

We use the sampling distribution chi-square uniform.

Degrees of freedom is 5.

(c)

We obtain, 0.010 < P-value < 0.025.   

(d)

Since, , we fail to reject the null hypothesis.

(e)

Based on the given data we can conclude that at the 1% level of significance, the evidence is insufficient to conclude that census distribution and the ethnic origin distribution of city residents are different.