Question

You need to design a relief valve for a new pressurized propane storage tank. As part of the design process, you need to calculate the maximum pressure inside the tank for any feasible “worst case” scenario. One of your design cases is that a fire breaks out beneath the tank, causing the liquid propane inside to rapidly heat up to 250°F. The tank is a rigid 10 ft3 vessel that holds 150 lbm of propane. What is the pressure inside the tank (in atm) for your fire case?

a. Using the ideal gas law

b. The van der Waals equation of state

c. The Peng-Robinson equation of state

Answer 1

a) PV = nRT

so P = nRT / V

and n = m/MM

first, we convert the lbm to grams:

1 lbm -------> 454 g: 150 * 454 = 68100 g

MM of propane (C₃H₈) = 12*3 + 8*1 = 44 g/mol

n = 68100 / 44 = 1547.73 moles

Now let's convert the temperature to K:

°C = 250 - 32 / 1.8 = 121.11 °C

K = 121.11 + 273 = 394.11 K

And the volume of ft³ to cm³ and then to mL and L:

10 ft³ * (30.48 cm/ft)³ * 1 mL/cm³ * 1 L/1000 mL = 283.17 L

now, using R = 0.0821 L atm / K mol we can use the ideal gas equation:

P = 1547.73 * 0.0821 * 394.11 / 283.17 = 176.85 atm

b) the Van der Waals equation is:

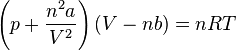
the values of a and b for propane are: 9.267 atm L²/mol and 0.089 L/mol so:

[P + 1547.73²*9.267/283.17²] (283.17 - 1547.73*0.089) = 1547.73*0.082*394.11

(P + 276.84)(145.42) = 50079.019

145.42P + 40258.072 = 50079.019

P = 50079.019 - 40258.072 / 145.42

P = 67.54 atm

I don't remember the Peng-Robinson equation, so I hope this helps.