Question

Suppose the following data are product weights for the same items produced on two different production lines.

Line 1	Line 2
13.9	13.5
13.3	14.2
14.0	14.4
13.6	14.0
13.8	14.9
13.4	13.7
13.1	14.8
13.9	14.3
12.6	14.7
14.8	14.1
	15.0
	14.6

Test for a difference between the product weights for the two lines. Use α = 0.05.

State the null and alternative hypotheses.

H₀: The two populations of product weights are identical.
H_a: The two populations of product weights are not identical.H₀: Median for line 1 − Median for line 2 < 0
H_a: Median for line 1 − Median for line 2 = 0    H₀: The two populations of product weights are not identical.
H_a: The two populations of product weights are identical.H₀: Median for line 1 − Median for line 2 ≤ 0
H_a: Median for line 1 − Median for line 2 > 0H₀: Median for line 1 − Median for line 2 ≥ 0
H_a: Median for line 1 − Median for line 2 < 0

Find the value of the test statistic.

W =

Find the p-value. (Round your answer to four decimal places.)

p-value =

State your conclusion.

Reject H₀. There is not sufficient evidence to conclude that there is a significant difference between the product weights for the two lines.Reject H₀. There is sufficient evidence to conclude that there is a significant difference between the product weights for the two lines.    Do not reject H₀. There is sufficient evidence to conclude that there is a significant difference between the product weights for the two lines.Do not reject H₀. There is not sufficient evidence to conclude that there is a significant difference between the product weights for the two lines.

Answer 1

As distribution of the weights is not specified,We perform Mann Whitney test in minitab for the above non parametric problem.

1. The null and alternative hypotheses.are :

H₀: The two populations of product weights are identical.
H_a: The two populations of product weights are not identical.

2. steps in minitab : stat, non parametric, Mann Whitney test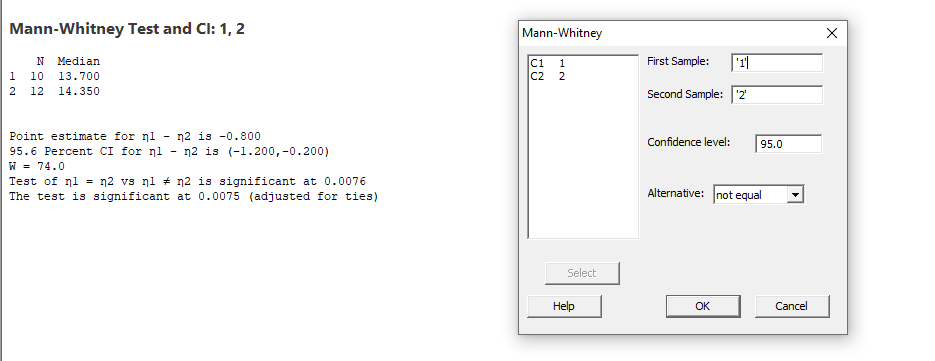

Value of the test statistic.

W =74

3. p-value =0.0075

4. Conclusion : As p-value=0.0075<0.05=alpha , we reject H0 i.e Reject H₀. There is sufficient evidence to conclude that there is a significant difference between the product weights for the two lines.