Question
In: Math
Use the dataset “ChickWeight”, available in R. Assume that each row is an observation of a...
Use the dataset “ChickWeight”, available in R. Assume that each row is an observation of a unique chick. weight is the weight of the chick. Diet is the diet treatment that the chick received. Assume that the distribution of chickweigts within each diet is approximately normal and variances are equal.
1. Construct a 95% confidence interval for the true mean weight of chicks.
2. Interpret the confidence interval in 1. in the context of the problem.
3. Construct a 99% confidence interval for the true mean weight of chicks.
4. Interpret the confidence interval in 2. in the context of the problem.
5. Write down the null and alternative hypothesis to determine if the mean weight of chicks is greater than 120.
6. Conduct a statistical test to determine if the mean weight of chicks is greater than 120. Use = 0.05.
7. Construct a box-and-whisker plot of weight by Diet. Label the graph and axes appropriately. (Hint: there should be 4 box-and whisker plots on one graph)
8. Write down the null and alternative hypothesis to determine if there is a difference in mean weight between diets.
9. Use an ANOVA to determine if there is a difference in mean weights between diets. Assume that all of the assumptions are met to perform the procedure. = 0.05.
10. If there is a difference in mean weights between diets, use a statistical procedure to rank the means where possible.
Solutions
Expert Solution
Solution1:
Rcode:
attach(ChickWeight)
dim(ChickWeight)
data(ChickWeight)
t.test(ChickWeight$weight)
output:
One Sample t-test
data: ChickWeight$weight
t = 41.208, df = 577, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
116.0121 127.6246
sample estimates:
mean of x
121.8183
95 percent confidence interval lies in
between 116.0121 and
127.6246.
2. Interpret the confidence interval in 1. in the context of the problem.
we are 95% confident that the true mean weight of chicks lies in
between 16.0121 and
127.6246.
3. Construct a 99% confidence interval for the true mean weight of chicks.
Rcode:
t.test(ChickWeight$weight,conf.level = 0.99)
output:
One Sample t-test
data: ChickWeight$weight
t = 41.208, df = 577, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
99 percent confidence interval:
114.1784 129.4583
sample estimates:
mean of x
121.8183
. Interpret the confidence interval in 2. in the context of the problem.
we are 99% confident that the true mean weight of chicks lies in between 114.1784 and 129.4583
Solution5:
5. Write down the null and alternative hypothesis to determine if the mean weight of chicks is greater than 120.
H0: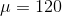
Ha: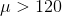
Related Solutions
R programming a. obtain the dataset ChickWeight b. obtain the mean weight at 16 days for...
Use R. Provide Solution and R Code within each problem. For this section use the dataset “PlantGrowth”,...
This problem is going to use the data set in R called "ChickWeight" that has 4...
This problem is going to use the data set in R called "ChickWeight" that has 4...
This problem is going to use the data set in R called "ChickWeight" that has 4...
Use the following dataset and assume all assumptions are met Provide all R code needed to...
3. For each dataset, what is the unit of observation? What is/are the variable(s) collected? State...
Fitting a linear model using R a. Read the Toluca.txt dataset into R (this dataset can...
ANSWER USING R CODE Using the dataset 'LakeHuron' which is a built in R dataset describing...
Please use R studio Dataset: IBM HR Analytics Employee Attrition & Performance dataset (you can download...
- Dissertation Proposal Form Proposed Dissertation Title: The title (tentative) should be precise to allow the reader...
- 1. Interest Rate Parity, Purchasing Power Parity, International Fisher deEffect Separated by more than 3,000 nautical...
- What is involved in collecting requirements for a project? Why is it often difficult to do?
- On January 1, 2018, Instaform, Inc., issued 10% bonds with a face amount of $54 million,...
- an electron 5.00 nm to the right of a proton. a second electron is 4.00 m...
- Project 2 This project has three components: Analyse Canada’s nominal and real GDP for last 5...
- A physics major is working to pay his college tuition by performing in a traveling carnival....
 milcah answered 3 weeks ago
milcah answered 3 weeks ago