Question

In: Math

2.1. The following data are an i.i.d. sample from a Cauchy(θ, 1) distribution: 1.77, -0.23, 2.76,...

2.1. The following data are an i.i.d. sample from a Cauchy(θ, 1) distribution: 1.77, -0.23, 2.76, 3.80, 3.47, 56.75, -1.34, 4.24, -2.44, 3.29, 3.71, -2.40, 4.53, -0.07, -1.05, -13.87, -2.53, -1.75, 0.27, 43.21.
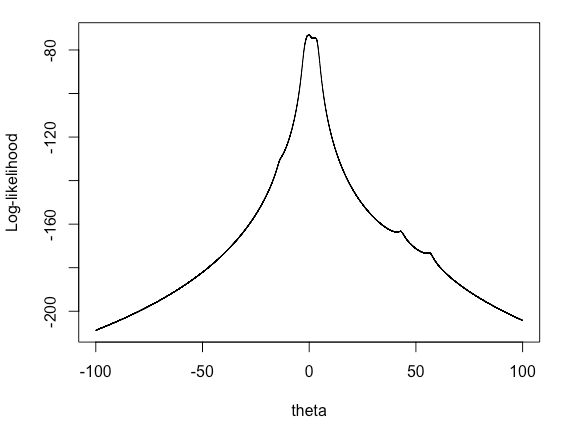
a. Graph the log likelihood function. Find the MLE for θ using the Newton–Raphson method. Try all of the following starting points: -11, -1, 0, 1.5, 4, 4.7, 7, 8, and 38. Discuss your results. Is the mean of the data a good starting point?
Please submit the code in R, thanks.

Solutions

Expert Solution

milcah answered 1 hour ago
Next > < Previous

Related Solutions

Suppose X1, ..., Xn are i.i.d. from an exponential distribution with mean θ. If we are...
Suppose X1, ..., Xn are i.i.d. from an exponential distribution with mean θ. If we are testing H0 : θ = θ0 vs Ha : θ > θ0. Suppose we reject H0 when ( X¯n/ θ0) > 1 + (1.645/ √n) (a) (10 points) Calculate the power function G(ζ). You may leave your answer in terms of the standard normal cdf Φ(x). (b) (5 points) Is this test consistent?
For a random variable X with a Cauchy distribution with θ = 0 , so that...
For a random variable X with a Cauchy distribution with θ = 0 , so that f(x) =(1/ π)/( 1 + x^2) for -∞ < x < ∞ (a) Show that the expected value of the random variable X does not exist. (b) Show that the variance of the random variable X does not exist. (c) Show that a Cauchy random variable does not have finite moments of order greater than or equal to one.
Suppose X1; : : : ; Xn is i.i.d Exponential distribution with density f(xjθ) = (1/θ)...
Suppose X1; : : : ; Xn is i.i.d Exponential distribution with density f(xjθ) = (1/θ) * e(-x/θ); 0 ≤ x < 1; θ > 0: (a) Find the UMVUE (the best unbiased estimator) of θ. (b) What is the Cramer-Rao lower bound of all unbiased estimator of all unbiased estimator of θ. Does the estimator from (a) attain the lower bound? Justify your answer. (c) What is the Cramer-Rao lower bound of all unbiased estimator of θ^2? 3 (d)...
Let X1. . . . Xn be i.i.d f(x; θ) = θ(1 − θ)^x x =...
Let X1. . . . Xn be i.i.d f(x; θ) = θ(1 − θ)^x x = 0.. Is there a function of θ for which there exists an unbiased estimator of θ whose variance achieves the CRLB? If so, find it
Let X1, . . . , Xn i.i.d. Uniform(θ, θ + 1). Show that: ˆθ1 =...
Let X1, . . . , Xn i.i.d. Uniform(θ, θ + 1). Show that: ˆθ1 = X¯ − 1 2 and ˆθ2 = X(n) − n n + 1 are both consistent estimators for θ.
Let X be a sample from population distribution Binomial(10, θ) and consider hypothesis test H0:θ=1, HA:θ̸=1....
Let X be a sample from population distribution Binomial(10, θ) and consider hypothesis test H0:θ=1, HA:θ̸=1. 22 Construct the test statistic T (X ) = |X 2 − 25|. Assume we observe x = 2. Find the p-value.
Suppose that (X1, · · · , Xn) is a sample from the normal distribution N(θ,...
Suppose that (X1, · · · , Xn) is a sample from the normal distribution N(θ, θ^2 ) with θ ∈ R. Find an MLE of θ.
Let X1,..., Xn be an i.i.d. sample from a geometric distribution with parameter p. U =...
Let X1,..., Xn be an i.i.d. sample from a geometric distribution with parameter p. U = ( 1, if X1 = 1, 0, if X1 > 1) find a sufficient statistic T for p. find E(U|T)
Let X1,...,Xn be i.i.d. N(θ,1), where θ ∈ R is the unknown parameter. (a) Find an...
Let X1,...,Xn be i.i.d. N(θ,1), where θ ∈ R is the unknown parameter. (a) Find an unbiased estimator of θ^2 based on (Xn)^2. (b) Calculate it’s variance and compare it with the Cram ́er-Rao lower bound.
Let X1, . . . , Xn be i.i.d. samples from Uniform(0, θ). Show that for...
Let X1, . . . , Xn be i.i.d. samples from Uniform(0, θ). Show that for any α ∈ (0, 1), there is a cn,α, such that [max(X1,...,Xn),cn,α max(X1,...,Xn)] is a 1−α confidence interval of θ.
ADVERTISEMENT
Subjects
ADVERTISEMENT
Latest Questions
ADVERTISEMENT