Question

two duopoly markets with a homogeneous good have a demand function of P= 100 - Q. Their costs are TC1=50q1 and TC2= 40q2. The two firms collude. What are the producer surplus, consumer surplus and profit?

Answer 1

P = 100 - q1 - q2

MC1 = dTC1/dq1 = 50

MC2 = dTC2/dq2 = 40

For firm 1,

TR1 = P x q1 = 100q1 - q1² - q1q2

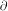MR1 = TR1/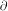q1 = 100 - 2q1 - q2

Setting MR1 = MC1,

100 - 2q1 - q2 = 50

2q1 + q2 = 50..........(1) [best response, firm 1]

For firm 2,

TR2 = P x q2 = 100q2 - q1q2 - q2²

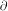MR2 = TR2/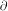q2 = 100 - q1 - 2q2

Setting MR2 = MC2,

100 - q1 - 2q2 = 40

q1 + 2q2 = 60..........(2) [best response, firm 2]

Multiplying (2) by 2,

2q1 + 4q2 = 120........(3)

2q1 + q2 = 50..........(1)

(3) - (1) yields:

3q2 = 70

q2 = 23.33

q1 = 60 - 2q2 [from (2)] = 60 - (2 x 23.33) = 60 - 46.66 = 13.34

Q = 13.34 + 23.33 = 36.67

P = 100 - 36.67 = 63.33

When Q = 0, P = 100

Total consumer surplus = (1/2) x (100 - 63.33) x 36.67 = (1/2) x 36.67 x 36.67 = 672.34

For firm 1,

Producer surplus (PS1) = (63.33 - 50) x 13.34 = 13.33 x 13.34 = 177.82

For firm 2,

Producer surplus (PS2) = (63.33 - 40) x 23.33 = 23.33 x 23.33 = 544.29

Total PS = PS1 + PS2 = 177.82 + 544.29 = 722.11

For firm 1,

Profit (Z1) = q1 x (P - MC1) = 13.34 x (63.33 - 50) = 13.34 x 13.33 = 177.82

For firm 2,

Profit (Z2) = q2 x (P - MC2) = 23.33 x (63.33 - 40) = 23.33 x 23.33 = 544.29

Total profit = Z1 + Z2 = 177.82 + 544.29 = 722.11