Question

4. Suppose from our class (with 25 students), we find the average GPA is 2.7, with standard deviation
0.4. Regard our class as a random sample from the whole university. Based on the information from our
class, can we believe at significance level 0.05, that the average GPA for all students can be at least 2.8?

Answer 1

The test of interest is

H₀: 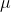=2.8 vs H₁: 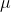>2.8

where 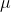is the average GPA for all students in the university

H₀ represents the hypothesis that the average GPA for all students of the university is at least 2.8

H₁ represents the hypothesis that the average GPA for all students of the university is more than 2.8

Given

n = sample size = 25

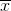= sample mean = 2.7

s = sample standard deviation = 0.4

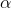= level of significance = 0.05

We see that population variance is unknown.

Therefore T = test statistic = ( 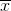- 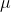) 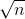/ s

t = observed value of T = (2.7 - 2.8)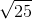 / 0.4 = -1.25

T ~ t_n-1 distribution i.e T ~ t₂₄ distribution

The test is a right-tailed test.

Therefore we reject H₀ if t > t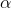_,n-1 i.e if t > t_0.05,24

From the t-distribution table we get the value that t_0.05,24 = 1.711

Thus t < t_0.05,24

Therefore we accept H₀

Thus; based on the information from our class, we can believe that at significance level 0.05, the average GPA for all students of the university is at least 2.8.