Question

1.         Parking Tickets – The Kaiserslautern police department claims that it issues an average of only 60 parking tickets per day.  The data below, reproduced in your Excel answer workbook,  show the number of parking tickets issued each day for a randomly selected period of 30 days.  Assume σ =13.42.   State the null and alternate hypotheses, as well as the claim, which (hint!) is in the null hypothesis.  Is there enough evidence to reject the group’s claim at  α = .05?   (As with all of these exercises, use the P-value method, rounding to 4 digits.)  (Hint:  so since we know the population standard deviation, use the standard normal distribution z-test .) (Monday class)

            79        78        71        72        69        71        57        60

            83        36        60        74        58        86        48        59

            70        66        64        68        52        67        67

            68        73        59        83        85        34        73

(Note:  You’ll find these data posted in Worksheet #1 of the Excel answer template.)

Answer 1

We will use minitab to solve the problem

The null and alternative hypothesis respectively will be:

H0 : The Kaiserslautern police department issues an average of only 60 parking tickets per day i.e mu =60

H1 : The Kaiserslautern police department doesn't issue an average of 60 parking tickets per day i.e mu not equals to 60

We will use one sample z test as the population standard deviation is known to be 13.42

alpha =0.05

Minitab steps : stat, basic statistics, one sample z test

Minitab output :

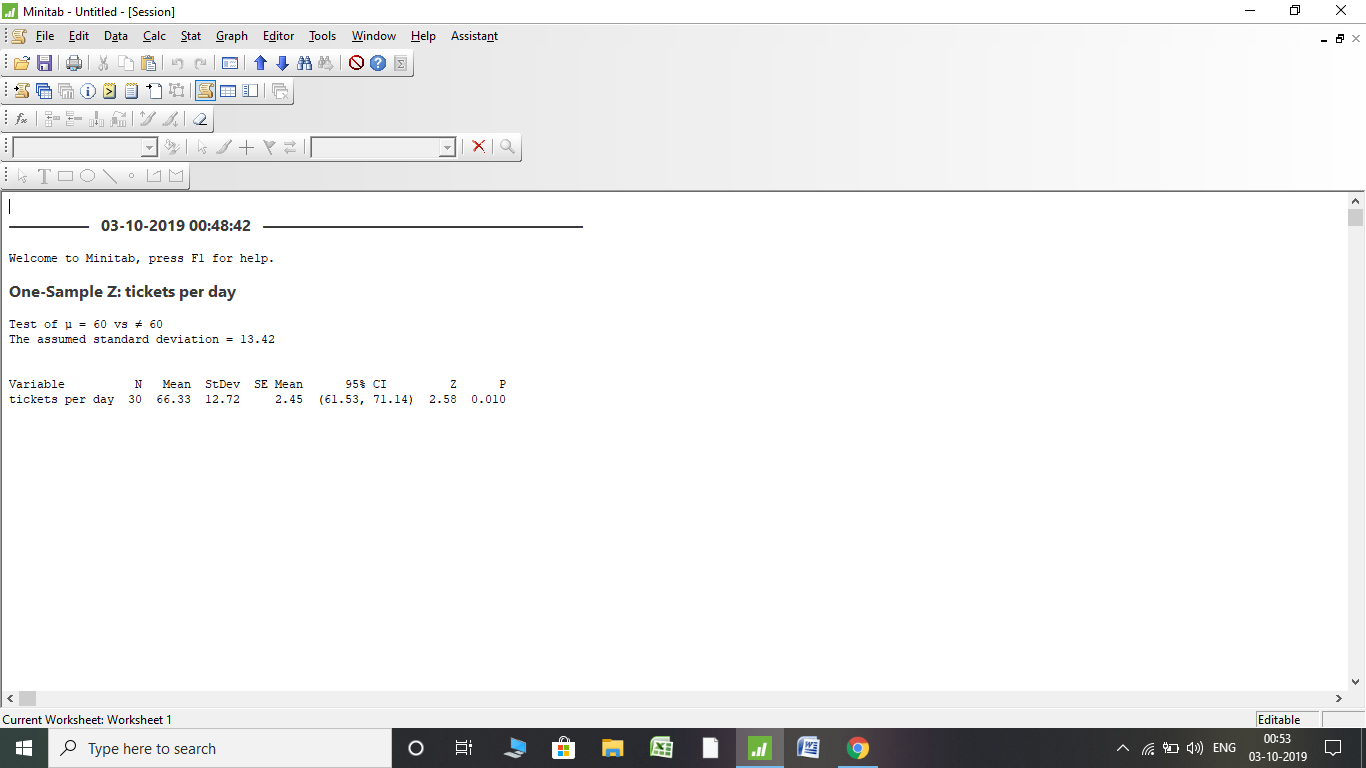
conclusion : As P-value =0.01 <alpha=0.05 we reject the null hypothesis and claim that The Kaiserslautern police department doesn't issue an average of 60 parking tickets per day i.e mu not equals to 60